В некоторых задачах машинного обучения объектами исследования могут быть множества — наборы объектов произвольного размера. Давайте рассмотрим возможные подходы к работе с множествами с помощью нейронных сетей.

Для систематизации знаний и закрепления полученной информации большинство обучающих курсов в OTUS заканчивается выполнением проекта. Это серьёзная работа, которая важна не только с точки зрения практической реализации полученных навыков, но и приносит реальную материальную пользу, так как становится своеобразным кейсом в портфолио.

У базовой архитектуры GANs есть одно существенное фундаментальное ограничение – подход не работает, если данные дискретные. 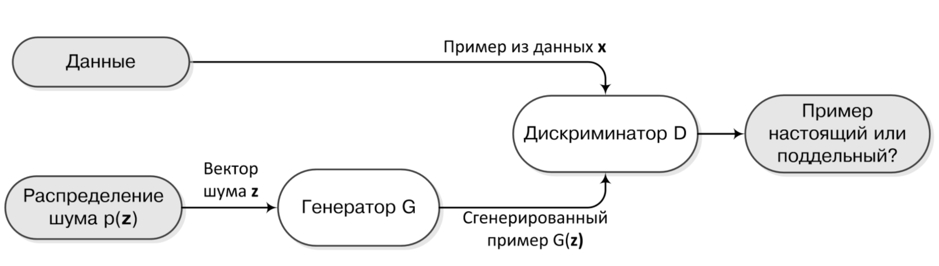Чтобы эффективно обновлять «веса», мы должны уметь пропускать градиент от Дискриминатора через примеры, порождённые Генератором. Понятно, что если данные представляют из себя бинарные вектора (например, bag of words или целые предложения), то ни о каком градиенте не может идти речи.

В январе 2017 года команда из Курантовского института математических наук и Facebook AI Research выложила в открытый доступ препринт статьи под названием «Wasserstein GAN».

Основное отличие этой статьи от большинства публикаций предлагающих очередное улучшение для Генеративных Состязательных Сетей заключается в фундаментальной теоретической базе. Авторы не просто демонстрируют очередной набор удачных изображений, порождённых GAN’ами, но и объясняют эффективность данного подхода с точки зрения теории. И в центре этой теории как раз и лежит расстояние Вассерштейна.

В предыдущем посте я рассказал о том, как делать свёртки на графах. Одним из ключевых моментов было понятие сообщения, которое задавалось как: 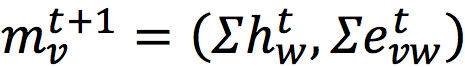Из-за того, что внутри вектора сообщения происходит независимое суммирование состояний соседних вершин и состояний рёбер, итоговая модель не может учитывать корреляции между вершинами и её рёбрами. Фактически нам бы хотелось, чтобы каждая соседняя вершина независимо от других передавала своё сообщение на очередном шаге.

Давайте рассмотрим свёрточные сети, но не обычные свёртки, а скорее их аналог для работы с графовыми данными. Граф — это сложный и непонятный для привычных нам нейронных сетей объект. Самый простой способ представить граф для работы с ним — записать его в виде матрицы смежности, в которой каждой вершине соответствует своя строка и свой столбец. В простейшем виде, такая матрица будет содержать только рёбра — единицы в клетках пересечения строк и столбцов, соответствующих связанным вершинам.

В первом посте я в общих чертах рассказал о том, что такое генеративные состязательные сети. Идея заставить соревноваться две нейронные сети выглядит очень просто и красиво, однако при реализации для конкретных задач обязательно возникают трудности. В этот раз я расскажу о том, как немножко изменить функции потерь так, чтобы стабилизировать процесс обучения.

На самом пике волне хайпа искусственного интеллекта уверенно держатся генеративные состязательные сети. Не все знают, но генеративные модели появились ещё в 18-ом веке, когда преподобный Томас Байес сформулировал своё знаменитое правило связавшее «приорное» и «постериорное» распределения.