Фрактальная размерность

Значимую роль в разработке подхода к анализу нелинейных динамических систем сыграла теория подобия. Теория подобия выдвигает понятия аттрактора для описания подобных объектов.
Теперь обратимся к критериям, описывающим геометрические свойства аттракторов. Необходимо отметить важность размерности, которая тесно связана с динамикой системы. Размерность играет основную роль в определении диапазона возможной динамической характеристики, например, размерность аттрактора дает числовую оценку числа активных степеней свободы рассматриваемой системы.
Геометрические объекты с размерностями, которые не являются целыми числами, выполняют фундаментальную роль в динамике хаотических систем. Такие объекты называются фракталами. Объект с нецелой размерностью обладает фрактальной размерностью.
Фрактальная размерность даёт новые возможности для изучения нелинейной динамики. Нелинейные системы обладают чувствительностью к начальным условиям в том смысле, что траектории, вначале близкие в пространстве состояний, могут под воздействием внешних и внутренних сил смешаться к различным аттракторам. В некоторых случаях эти аттракторы соответствуют неподвижным точкам или предельным циклам, в других — такие аттракторы могут быть хаотическими.
Как известно, аттрактор характеризуется своим бассейном притяжений, и для многих нелинейных систем границы бассейнов притяжения представляют собой сложные геометрические объекты, которые лучше определяются фрактальной размерностью. Эти границы в сильной степени обладают сильной «колеистостью», что приводит к чувствительности от начальных условий: небольшое изменение в начальных условиях может сдвинуть траекторию непредсказуемым образом от одного бассейна притяжения к другому.
В современных экономических рядах эмпирически отмечается тот факт, что фрактальная размерность меняется по ходу ряда. Изменение фрактальной размерности приводит к тому, что поведение значений ряда усложняется ещё в большей степени. Подобное усложнение также демонстрирует некомпетентность традиционных методов анализа и прогнозирования.
Б. Мандельброт даёт следующее определение фракталам: «фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». Существуют различные способы расчёта размерности.
Методы расчёта фрактальной размерности сводятся или к подсчету степени изрезанности ряда с помощью окружностей определённого радиуса (метод Ричардсона), или к определению числа ячеек в пространстве, занимаемом фрактальной кривой (емкостная размерность), или посредством так называемой корреляционной суммы (корреляционная размерность), или к расчёту показателя Херста H.
В настоящее время фрактальный анализ, как один из инструментов, предлагаемый теорией хаоса, применяется успешно во многих областях. Основной характеристикой самоподобных структур является фрактальная размерность D. Данная характеристика была предложена Хаусдорфом в 1919 году. Позднее Мандельброт доработал некоторые идеи Хаусдорфа.
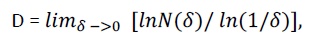
N(δ) – минимальное число шаров радиуса δ, которые покроют это множество. Часто на практике при попытке вычислить показатель D возникают проблемы, связанные с тем, что временной ряд всегда имеет минимальный масштаб для δ. Показатель D получил название показатель Хаусдорфа (размерность Хаусдорфа). Однако для надежного вычисления требуется большой объем данных для проведения расчета. Иначе результаты могут получиться нерепрезентативными.
Если известно достаточное количество показателей Ляпунова, то можно оценить ляпуновскую размерность аттрактора по формуле Каплана-Йорке:

Материал является отрывком из научной работы «Теория нелинейной динамики».
Хотите знать больше? Добро пожаловать на мой Телеграм-канал!

