Пространство элементарных исходов
Давайте представим, что из некоторого случайного эксперимента, который можно повторять многократно (допустим, подбрасывание монетки или кубика), можно извлечь какую-нибудь формализуемую информацию (как известно, выпадет орел или решка). Эту формализуемую информацию можно назвать элементарным исходом, при этом есть целесообразность рассматривать множество всех элементарных исходов (это множество обычно обозначают буквой Ω (Омега).

От чего же зависит структура этого пространства? Разумеется, от природы проводимого эксперимента. Если мы возьмем, к примеру, стрельбу по большой круговой мишени, то пространством элементарных исходов в данном случае станет круг, который для удобства размещен с центром в нуле, а исходом будет являться точка в этом круге.
Попадание в «десятку» — концентрический круг небольшого радиуса с мишенью -- это событие, выпадение соответствующего числа на кубике -- тоже событие, а в целом можно говорить о множестве элементарных исходов — событий.
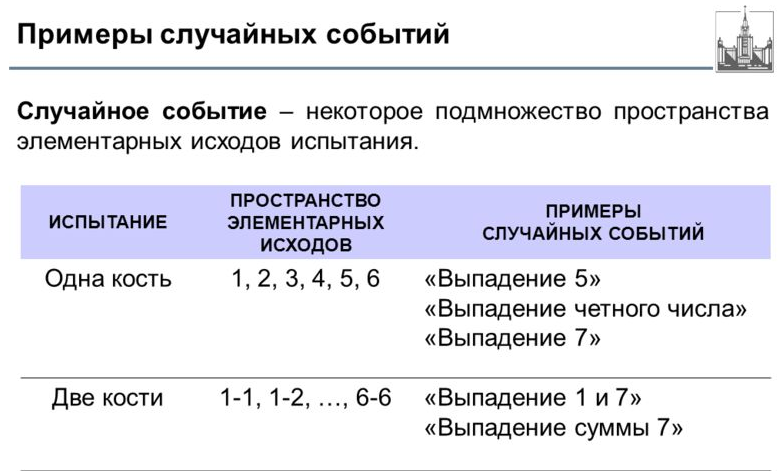
С точки зрения дискретности, вроде бы, все относительно просто: можно получить любое событие за конечное время, как включая, так и исключая элементарные исходы.

Если же говорить о непрерывном случае, то все намного сложнее: потребуется некоторое семейство множеств (семейство множеств — индексированный аналог системы множеств). При этом в той же алгебре множества можно пересекать и объединять, причем результат операции будет находиться. И это очень важное математическое свойство, то есть минимальное семейство состоит всего лишь из 2-х множеств — пространства элементарных исходов и пустого множества.
По материалам статьи «Математика для программистов: теория вероятностей».

