Математика для ИИ: операции с матрицами

Из операций с матрицами можно выделить транспонирование, псевдоинверсию, преобразование в скаляр, умножение на вектор и умножение на обратную матрицу. Знание этих операций пригодится вам в контексте понимания принципов работы ИИ.

Транспонирование матрицы

После транспонирования мы получим так называемую транспонированную матрицу. Можно сказать, что это будет зеркальным отображением матрицы по главной диагональной линии (начинается в левом верхнем углу и идёт в нижний правый угол).

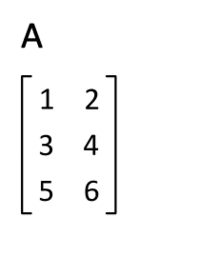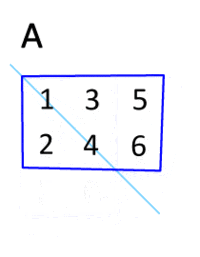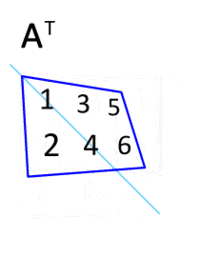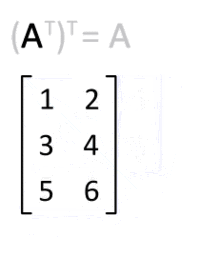
Представьте, что у нас есть матрица A. Транспонированной будет являться матрица А^т( А^t, А^tr). Вдобавок к этому, такую матрицу мы сможем получить, если запишем ряды матрицы A в виде столбцов матрицы A^т, а столбцы — в виде рядов.

Умножаем единичную матрицу на вектор

Понятие единичной матрицы вам должно быть знакомо. Если умножить такую матрицу на вектор, то значения вектора не изменятся. На картинке ниже элементы главной диагонали единичной матрицы равны 1, остальные — 0:

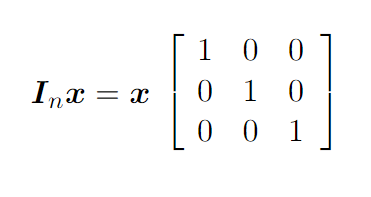
Следует отметить, что диагональная матрица очень похожа на единичную. Все её элементы, кроме находящихся на главной диагонали, равняются нулю. Однако в отличие от единичной, здесь на главной диагонали матрицы элементы не равны 1. Следовательно, можно сказать, что единичная матрица является видом диагональной матрицы. Такие матрицы весьма полезны при решении ряда алгоритмов.

Умножаем на обратную матрицу

Обратную матрицу определяют так:

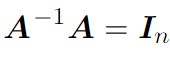
Умножив матрицу A на обратную ей матрицу A со степенью -1, мы получим единичную матрицу. Говоря об обратной матрице, можно вспомнить обратное число. Например, для числа a обратным будет 1/a. Если же обычное число мы умножим на обратное ему, мы получим единицу: a * 1/a = 1. То же самое и с матрицами. Но тут стоит учесть, что данное утверждение справедливо лишь для квадратных матриц.

Псевдоинверсия Мура-Пенроуза

Когда нам нужно выполнить операцию для неквадратных матриц, подойдёт псевдоинверсия Мура-Пенроуза:

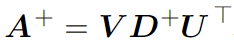
Здесь U, D и V — сингулярное разложение нашей матрицы A.

Псевдоинверсия D⁺ матрицы D формируется путём взятия элементов, которые обратны элементам матрицы, а также её дальнейшим транспонированием. Однако следует быть осторожным с концепцией обратной матрицы A^-1, ведь пока она больше применяется в теории, чем на практике. Ситуация обусловлена тем, что вычислительные способности даже самых современных компьютеров дают лишь приблизительный ответ.

Преобразуем матрицу в скаляр

Случается, что необходимо преобразовать матрицу в скаляр, для чего надо найти определитель, обозначаемый det(A) либо |A|. Это преобразование возможно лишь с ними, ниже вы увидите пример с матрицей 2×2:

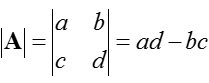
Тут же следует сказать несколько слов о линейной зависимости. Набор векторов тогда считается линейно зависимым, когда хоть один вектор может быть представлен в виде комбинации других векторов из набора. В обратном случае набор является линейно независимым. Как правило, векторы x и y можно считать линейно независимыми, только когда значения для скаляров a и b, удовлетворяющих ax + by = 0, равняются a = b = 0.

Источник — «Mathematics for Artificial Intelligence – Linear Algebra»