Метод Box-Counting

Это известный алгоритм, который позволяет оценить эффект входной информации на наблюдаемый выходной параметр. Пространство переменных X и Y разбивается на ячейки. Количество заполненных ячеек будет использоваться для оценки вероятностного распределения входных параметров.
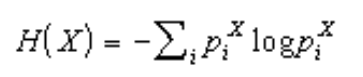
Чем больше энтропия переменной, тем менее предсказуемо её значение. Если значения примеров находятся в одной ячейке, то их энтропия равна 0.
Предсказуемость случайного вектора У, обеспечиваемое знанием другой случайной величины Х, характеризуется кросс-энтропией:
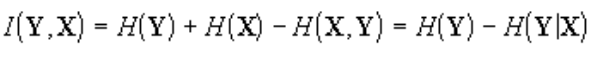
Кросс-энтропия равна логарифму отношения типичного разброса значений переменной к типичному разбросу этой переменной, но при известном значении переменной Х.
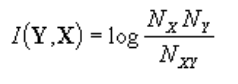
Чем больше кросс-энтропия, тем больше определённости вносит знание значения Х в предсказание значения переменной. Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными.
Таким образом, данная методика даёт наиболее общий метод определения значимости входов, позволяя также оценивать степень предсказуемости выходов.
Метод Box-counting, как уже было описано выше, определяет, сколько ячеек размером ε содержат точки корреляционной размерности ряда, т. е. может быть записана формула:
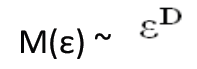
В данной формуле D – корреляционная размерность.
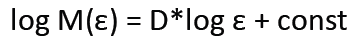
Данный метод относительно прост для его применения на практике. Однако данный метод практически не применим для анализа финансовых временных рядов. Для того, чтобы достичь хотя бы минимальной надёжности выполнения алгоритма Box-Counting, требуется проводить анализ по нескольким сотням тысяч наблюдениям в ряду. Такое ограничение на длине ряда и невозможность рассчитывать локальную корреляционную размерность является крайне сильным недостатком данного метода.
Хотите знать больше? Добро пожаловать на мой Телеграм-канал!

