Алгоритм Грассбергера – Прокаччиа: вычисляем корреляционную размерность

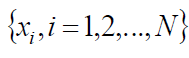Основой данного метода является восстановление иного, но «похожего» на исходный аттрактор последовательным сдвигом. Алгоритм Грассбергера – Прокаччиа состоит в следующем: пусть мы имеем набор m-мерных векторов состояния Векторы получены из численного решения уравнений динамики. Используя некоторое (малое) ℇ, можно применить наш набор данных для оценки C_m(ℇ): 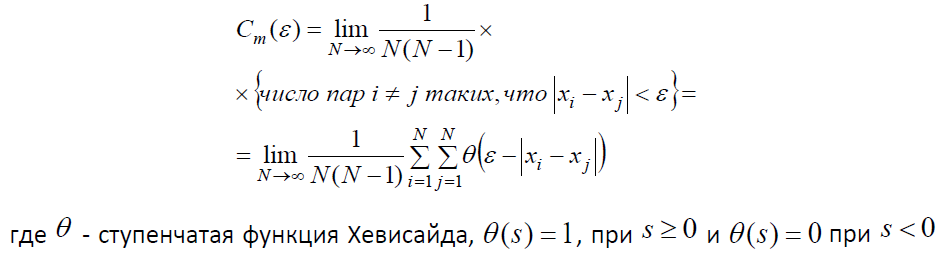Величина C_m(ℇ) — корреляционный интеграл, служит (при достаточно больших N, обычно тысячи или десятки тысяч) статистической оценкой суммы C(ℇ), где индекс m показывает размерность пространства вложения. C(ℇ) показывает вероятность того, что временной ряд содержит пару точек, расстояние между которыми не превышает r. Для вычисления корреляционной размерности, для вложения размерности m, проводят расчёт C_m(ℇ) при различных (ℇ) и строят линейную регрессию в двойных логарифмических координатах logC_m(ℇ)и logℇ. Тангенс угла наклона прямой и будет являться оценкой корреляционной размерности D_c для вложения размерности m. 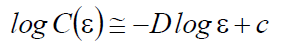Другая форма записи алгоритма Грассбергера – Прокаччиа может быть осуществлена следующим образом: Для оценки корреляционной размерности D используют линейную аппроксимацию зависимости на участке с наибольшей линейностью. Чем ниже корреляционная размерность ряда, тем меньшее число параметров задействовано в описании системы. Как уже говорилось выше, вычисление корреляционной размерности помогает при анализе временных рядов на предмет поиска в этих рядах сложных закономерностей. Для определения таких закономерностей необходимо определить количество всех переменных системы. Для этого существуют методы, позволяющие вычислять количество параметров. Алгоритм Грассбергера – Прокаччиа является устойчивым к шумам внутри ряда. Данный метод легко применим для анализа финансовых временных рядов. Точность оценок корреляционной размерности данным методом очень высока. Однако данный алгоритм не позволяет вычислять локальных оценок корреляционной размерности ряда. Для эффективной работы алгоритма требуется большой объём наблюдений в ряде. _Хотите знать больше? Добро пожаловать на мой [Телеграм-канал](http://t.me/datastreet)!_