Критерий Акайке и Шварца
На сегодняшний день наиболее распространёнными методами по оценке качества модели являются критерии Акайке (AIC) и Шварца (BIC). Оба эти критерия построены приблизительно одинаково.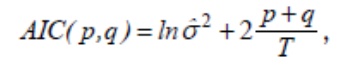
где Т – число наблюдений в ряду, Р – количество запаздываний основных параметров, q – количество запаздываний ошибок. Фактически p + q – это оптимальное количество параметров в модели.
Критерий Шварца имеет следующий вид:
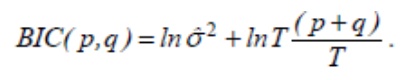
Минимально значение критерия позволяет определить оптимальное количество параметров в модели. Чем меньше критерий, тем выше качество модели.
Замечу, что в отличие от коэффициента детерминации модели, ничего нельзя сказать о диапазоне значений. Не существует абсолютной шкалы изменений данного показателя, возможно проведение только относительного сравнения по данным показателям.
Критерий Акайке основывается на обобщении принципа максимального правдоподобия. Это означает, что в приведённом выражении случайное возмущение в модели считается гауссовым. Было показано, что критерий Акайке переоценивает порядок модели.
Критерий Шварца основан на байесовском подходе и имеет более фундаментальные теоретические обоснования. Оценка, получаемая с помощью данного показателя, считается состоятельной. Однако на практике чаще применяют критерий Акайке.
Для оценки корреляционной размерности возможно применение следующего метода. С помощью нейросетей происходит создание моделей временного ряда с различным количеством параметров. Далее полученные модели сравниваются по критерию Акайке или Шварца. Модель с минимальным значением критерия среди прочих моделей считается оптимальной. Количество параметров в данной модели позволит получить оценку корреляционной размерности модели.
Данные критерии просты в применении. Они не требовательны к длине ряда, способны давать надёжные оценки при любой длине ряда. Однако недостатком данных критериев является то, что не существует меры абсолютного сравнения результатов применения данных критериев. Возможно только их относительное сравнение, что делает затруднительным применение данных критериев в скользящем подходе к анализу временного ряда.
Материал является отрывком из научной работы «Теория нелинейной динамики».
Хотите знать больше? Добро пожаловать на мой Телеграм-канал!
