Вычисление специального факториала по модулю p за O(p log N)

Рассмотрим задачу вычисления формул, состоящих из дробей, где в числителе и в знаменателе присутствуют факториалы (например, биномиальные коэффициенты).

Будем вычислять факториалы по некоторому небольшому простому модулю p, пропуская сами множители p, потому что в дробях множители p сократятся, и результат будет взят по модулю p.

Видно, что формула делится на несколько блоков одинаковой длины, за исключением последней части:

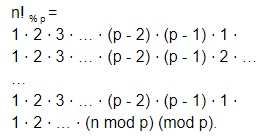Одинаковые блоки содержат общую часть (p - 1)! mod p, что по теореме Вильсона равно p - 1. Чтобы перемножить эти общие части, p - 1 нужно возвести в степень по модулю p (как рассказывается в нашей статье «Быстрое возведение в степень»), однако результат всегда будет 1 или p - 1 в зависимости от чётности показателя.

Значение последнего блока можно вычислить отдельно за O(p). Рассмотрим последние элементы блоков:

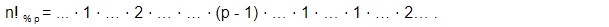
Задача свелась к задаче меньшей размерности (осталось n / p блоков). Программа:

    def factmod(n, p):
        res = 1
        while n > 1:
            res = (res * (p - 1 if int(n / p) % 2 else 1)) % p
            for i in range(2, n % p + 1):
                res = (res * i) % p  
            n = int(n / p)
        return res % p

Есть вопросы? Напишите в комментариях!