Решето Эратосфена: просеиваем простые числа

Что такое решето Эратосфена, знает сегодня, пожалуй, любой школьник, интересующийся математикой. Но не всякий знает, какова алгоритмическая сложность этого «просеивателя».

Напомним условие задачи

Необходимо найти все простые числа, меньшие или равные заданному числу N.

Запишем в ряд все числа от 1 до N и будем вычёркивать оттуда все числа, кратные двойке, но больше двойки, затем, все числа, кратные тройке, но больше тройки и т. д.

Если число уже вычеркнуто, пропускаем его и переходим к следующему. Так мы продолжаем, пока не дойдем до N. В итоге у нас останутся невычеркнутыми только простые числа.

Почему так?

Потому что оставшиеся числа не делятся ни на что, кроме самих себя и единицы. Это легко доказать методом от противного. Допустим, осталось число n и оно делится на некоторое k, такое, что 1 < k < n. Значит, оно должно было быть вычеркнуто, когда вычёркивали числа, делящиеся на k. А оно у нас не вычеркнулось.

Оптимизации

Можно просеивать только нечётные числа, ибо чётные — заведомо составные. Можно просеивать только числа до √N.

Теперь оценим потребление памяти и вычислительную сложность этого алгоритма

По памяти этот алгоритм требует O(N), потому что размер целевого массива N и никакой дополнительной памяти не используется.

Оценим теперь его вычислительную сложность (интересно, что оптимизации на асимптотическую сложность не влияют, а уменьшают только коэффициент). Для каждого простого p вычёркиваем числа N / p раз. Общее число действий, которые мы производим, равно сумме: 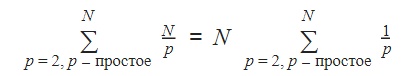Примем как данность, что число простых чисел, меньших либо равных N, приблизительно равно N / ln N, следовательно, k-e простое число приблизительно равно k ln k.

Оценим сумму:

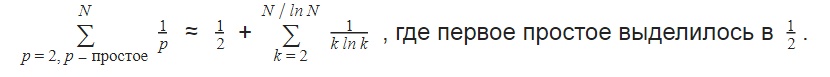
Оценим новую сумму как интеграл:

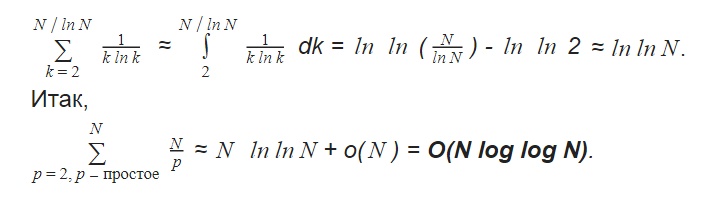
Интересно, знал ли об этом Эратосфен?