Создаём нейронную сеть на Python с нуля
Для начинающего Data Scientist-а очень важно понять внутреннюю структуру нейронной сети. Это руководство поможет вам создать собственную сеть с нуля, не используя для этого сложных учебных библиотек, к коим относится, например, TensorFlow.
Что такое нейронная сеть?
Очень часто в статьях по нейронным сетям авторы описывают их, проводя параллели с мозгом. Описать нейронную сеть можно и в качестве математической функции, отображающей заданный вход в желаемый результат.
Итак, нейронные сети включают в себя следующие компоненты: — х, входной слой; — ŷ, выходной слой; — набор весов и смещений между каждым слоем W и b; — произвольное количество скрытых слоев; — выбор функции активации для любого скрытого слоя σ (в данной статье будем использовать функцию активации Sigmoid). На диаграмме, представленной ниже, отображена архитектура 2-слойной нейронной сети (учтите, что входной уровень, как правило, исключается во время подсчёта числа слоев).
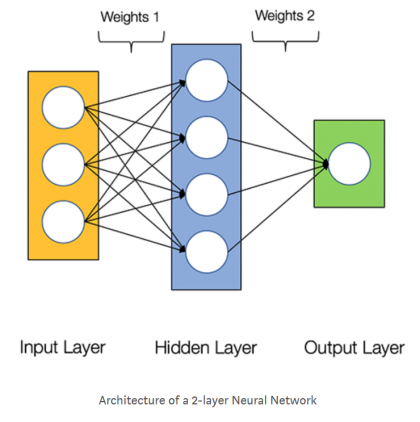
Идём дальше. Создание класса Neural Network на «Питоне» выглядит следующим образом:
class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(y.shape)
Обучение нейронной сети
Выход ŷ простой 2-слойной нейронной сети:
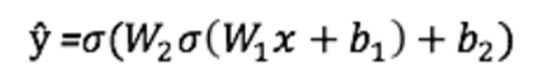В уравнении, которое приведено выше, веса W и смещения b — единственные переменные, влияющие на выход ŷ. Разумеется, правильные значения для смещений и весов определяют точность предсказаний. А сам процесс тонкой настройки смещений и весов на основании входных данных называют обучением нейронной сети.
В обучающем процессе каждая итерация включает ряд шагов: 1) вычисление прогнозируемого выхода ŷ (прямого распространения); 2) обновление смещений и весов (обратное распространение).
Процесс обучения хорошо иллюстрирует последовательный график:
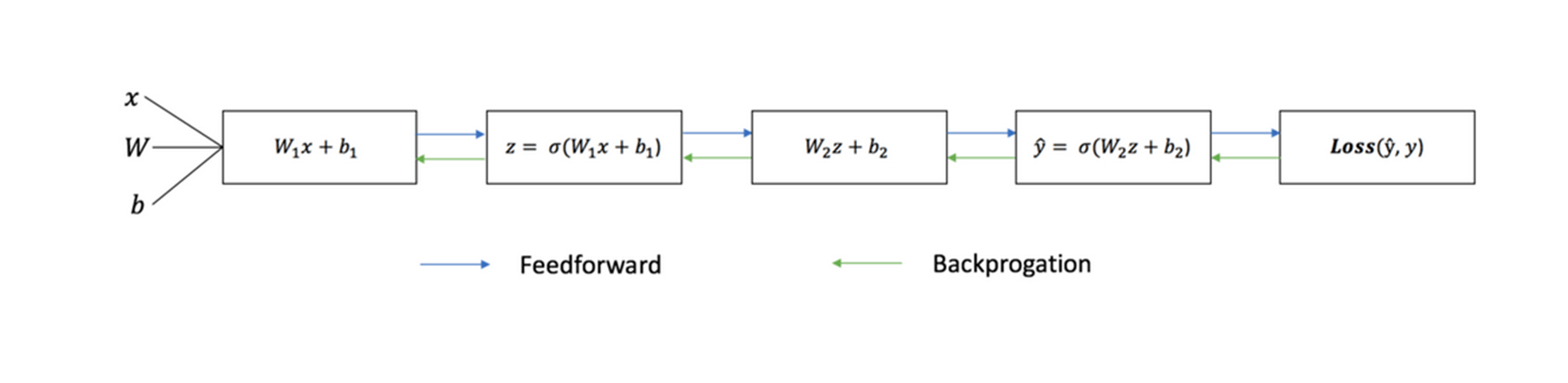
Прямое распространение
Как видно на графике, прямым распространением называют несложное вычисление, причём для базовой двухслойной нейронной сети вывод задаётся следующей формулой:
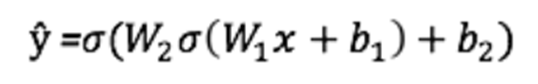Давайте теперь добавим в наш код функцию прямого распространения. Для простоты предполагается, что смещения равны нулю.
class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2))
Чтобы оценить «добротность» наших прогнозов, воспользуемся функцией потери.
Функция потери
Вообще, существует много доступных функций потерь, и на выбор влияет характер нашей проблемы. Мы же будем применять в качестве функции потери сумму квадратов ошибок:
Суммой квадратов ошибок называют среднее значение разницы между каждым фактическим и прогнозируемым значением.
Что касается цели обучения, то она как раз в том и состоит, чтобы найти набор смещений и весов, который минимизирует вышеупомянутую функцию потери.
Обратное распространение
Когда ошибка нашего прогноза, то есть потери, измерены, необходимо отыскать способ обратного распространения ошибки, обновив смещения и веса. И чтобы узнать подходящую нам сумму, нужную для корректировки смещений и весов, требуется знать производную функцию потери по отношению к смещениям и весам.
Здесь давайте вспомним, что производной функции называют тангенс угла наклона функции.
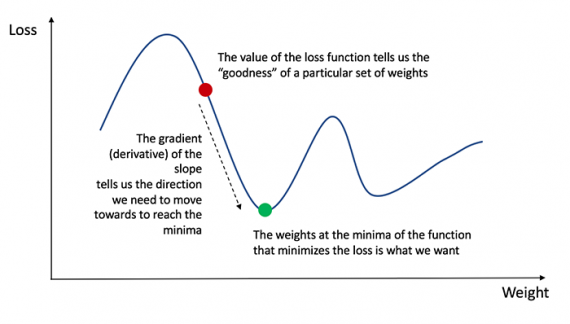Раз есть производная, можно просто обновить смещения и веса, уменьшив либо увеличив их (смотрите диаграмму выше). Это называют градиентным спуском.
Однако мы не сможем непосредственно посчитать производную функции потерь по отношению к смещениям и весам, ведь уравнение функции потерь не включает в себя смещения и веса. На помощь приходит правило цепи:
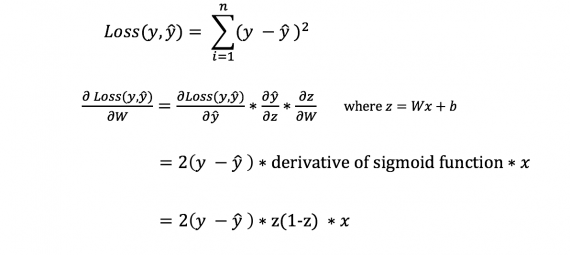Да, это было громоздко, зато позволило нам получить то, что необходимо — производную функции потерь (наклон) по отношению к весам. А значит, можно регулировать веса.
Теперь добавим в наш код функцию обратного распространения (backpropagation):
class NeuralNetwork: def __init__(self, x, y): self.input = x self.weights1 = np.random.rand(self.input.shape[1],4) self.weights2 = np.random.rand(4,1) self.y = y self.output = np.zeros(self.y.shape) def feedforward(self): self.layer1 = sigmoid(np.dot(self.input, self.weights1)) self.output = sigmoid(np.dot(self.layer1, self.weights2)) def backprop(self): # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1 d_weights2 = np.dot(self.layer1.T, (2*(self.y - self.output) * sigmoid_derivative(self.output))) d_weights1 = np.dot(self.input.T, (np.dot(2*(self.y - self.output) * sigmoid_derivative(self.output), self.weights2.T) * sigmoid_derivative(self.layer1))) # update the weights with the derivative (slope) of the loss function self.weights1 += d_weights1 self.weights2 += d_weights2
Проверка работы нейронной сети
Когда полный код для выполнения обратного и прямого распространения есть, можно рассмотреть нейросеть на примере и посмотреть, как всё работает.
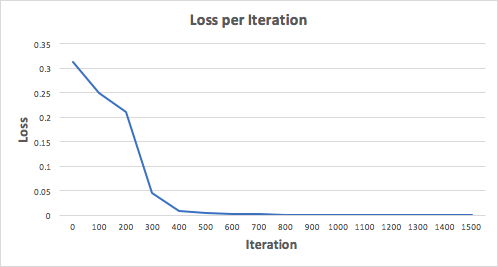
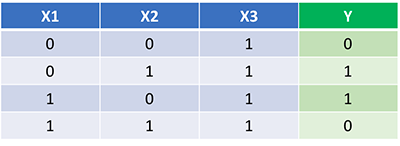На картинке вы видите идеальный набор весов. И наша нейронная сеть должна изучить его. Давайте потренируем сеть на 1500 итераций. Рассматривая график потерь на итерациях, можно заметить, что потеря монотонно уменьшается до минимума. Всё это соответствует алгоритму спуска градиента, о котором уже упоминали.
Теперь посмотрим на вывод (окончательное предсказание) после 1500 итераций:
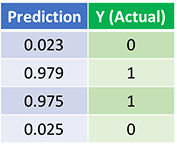Итак, мы сделали это! Алгоритм обратного и прямого распространения показал успешную работу нейросети, а сами предсказания сходятся на истинных значениях. Но нужно добавить, что существует незначительная разница между фактическими значениями и предсказаниями. Это нормально и даже желательно, т. к. предотвращается переобучение, позволяя нейросети лучше обобщать невидимые данные.
