Глубокое обучение на множествах. Часть 2

В некоторых задачах машинного обучения объектами исследования могут быть множества — наборы объектов произвольного размера. В предыдущей заметке я рассказывал о том, как работать со множествами когда их нужно предсказывать, а в этой заметке мы поговорим о задаче поиска изображения на основе множества тегов.

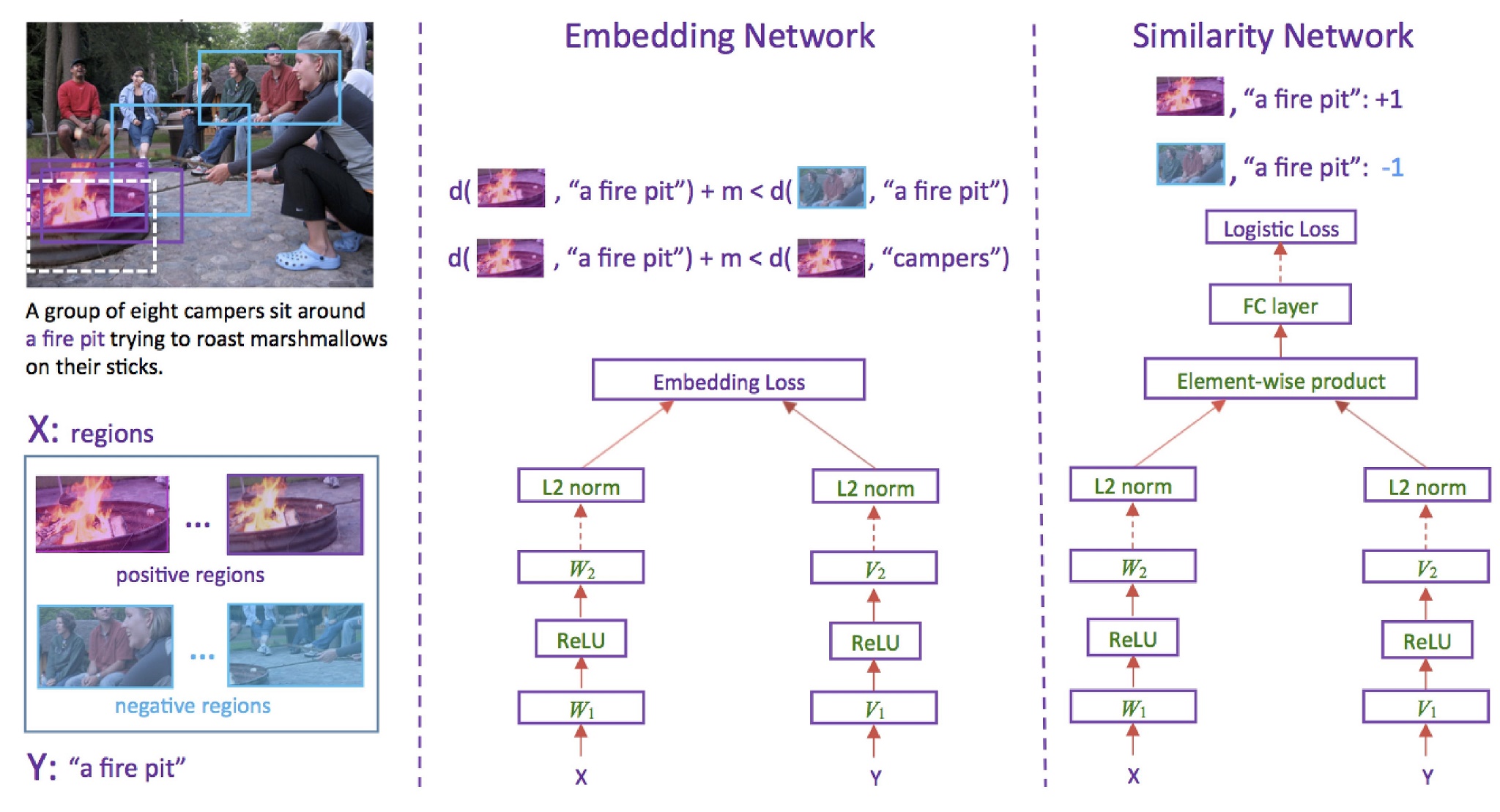В случае с поиском изображения архитектура нейронной сети может быть, например, такой как в статье «Learning Two-Branch Neural Networks for Image-Text Matching Tasks». Нейронная сеть в этом случае будет иметь две «головы»: одна преобразует текстовое описание картинки в вектор признаков, вторая — само изображение. Целью обучения будет минимизировать расстояние между соответствующими друг другу парами (описание, изображение) и максимизировать в обратном случае.

А если у нас набор тегов?

Если вместо текстового описания у нас набор тегов, мы, следуя примеру из прошлой заметки, можем рассматривать этот набор как последовательность и обрабатывать её с помощью рекуррентной нейронной сети. Причём теперь отсутствие порядка во множестве тегов может быть использовано для аугментации тренировочного сета.

По сути, для каждого изображения с n-тегами мы можем получить n! обучающих примеров. Правда, это не гарантирует независимости результата от порядка, но всё же станет некоторым приближением к решению проблемы порядка.

Поговорим о пуллинге

Наиболее популярным способом обработки сетов является применение пуллинга — того самого, который используется в глубоких свёрхточных сетях, а точнее, его одномерных братьев. Первые слои сети обрабатывают каждый тег независимо, после чего вектора признаков от всех тегов, например, усредняются.

Помимо усреднения, можно выбирать максимумы или минимумы каждого из параметров по этим векторам. Полученный вектор может быть пропущен ещё через несколько слоев нейронной сети или быть использован в качестве вектора признаков как есть. А в статье «Deep Sets», представленной на конференции NIPS 2017, этот подход обобщается на класс функций инвариантных и эквивариантных к перестановкам. Кстати, среди соавторов этой статьи есть и наш соотечественник Руслан Салахутдинов — один из самых известных учёных в области науки о данных.

Помимо описанных подходов для работы с множествами, в рамках своего курса я разберу статью под названием «PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation», посвящённую классификации и сегментации 3D-сцен, представленных множеством точек.

Задать вопрос всегда можно в комментариях!