Математика для ИИ: базовые термины линейной алгебры

Данная статья даст вам представление о базовых концепциях линейной алгебры — необходимых основах для всех, кто профессионально интересуется машинным обучением, искусственным интеллектом и нейронными сетями. Помните, что многие концепции, используемые в вышеописанных областях, основаны на математических принципах и были открыты более 50 лет назад.

По большему счёту, вся линейная алгебра строится вокруг нескольких понятий — это скаляры, векторы, матрицы и тензоры. Эти понятия очень важны для Machine Learning, ведь с их помощью можно абстрагировать модели и данные. При этом каждую запись в каком-либо наборе данных можно представить в виде вектора в многомерном пространстве, а параметры нейросетей абстрагируются, как матрицы. Так как каждое из понятий специфично по своему, рассмотрим их более подробно.

Скаляр

Скаляр, в отличие от матрицы или вектора, является всего лишь числом. Скаляры определяются как элементы поля и предназначены для описания векторного пространства, а несколько скаляров формируют вектор. Скаляры бывают представлены различными типами чисел: действительными, вещественными, натуральными. Обозначаются они прописными и строчными буквами греческого и латинского алфавитов:

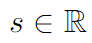
Вектор

Вектор представляет собой упорядоченный массив скаляров, причём скаляры выступают тут в виде координат точек в пространстве. Скопление векторов образует векторное пространство. Векторы можно складывать, перемножать, масштабировать. Обозначаются векторы жирным шрифтом, при этом у каждого элемента есть индекс.

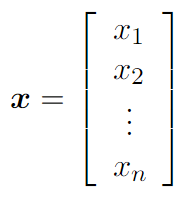
Матрица

Матрица — 2-мерный массив скаляров. Матрица обозначается в верхнем регистре жирным шрифтом. Допустим, матрица из вещественных чисел, с m рядов и n столбцов будет записана так:

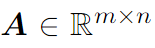Так как матрица — это 2-мерный массив, её элементы имеют 2 индекса:

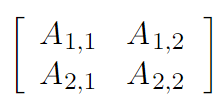Две матрицы можно складывать и вычитать друг с другом, но только в том случае, когда у них одинаковое число столбцов и рядов. Что касается умножения, то 2 матрицы можно перемножать, если число столбцов 1-й матрицы соответствует числу рядов 2-й. К примеру, можно перемножить матрицу A размера m, n с матрицей B размера n, p. В итоге получим матрицу C размера m, p. Вот, как будет выглядеть формула умножения:

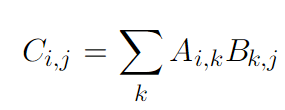Также стоит добавить, что матричное произведение ассоциативно и дистрибутивно:

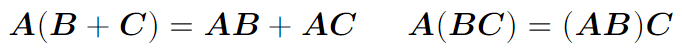Но в некоторых случаях нам надо перемножать элементы матриц между собой. Речь идёт об операции под названием произведение Адамара (обозначают A ∘ B). Кроме того, матрицы можно умножать на скаляры и векторы. Интересный факт: произведением вектора и матрицы будет вектор:

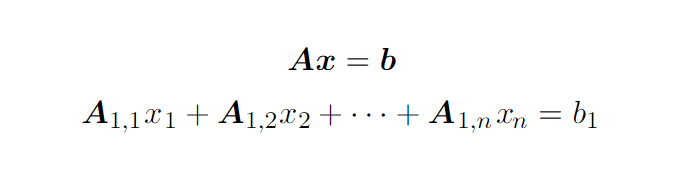
Тензор

Тензор представляет собой многомерный массив чисел. Как правило, в тензоре более 2-х измерений, поэтому его можно изобразить, как многомерную сетку, состоящую из чисел. Но по большему счёту, матрицы — это те же тензоры, но они 2-мерные, вот и все отличия. Что касается тензоров, то они получили известность в том числе и благодаря ML-фреймворку TensorFlow.

В следующей части этой статьи мы продолжим разговор о линейной алгебре в контексте ИИ. Следите за новостями блога!

Источник — «Mathematics for Artificial Intelligence – Linear Algebra»