Ансамбли моделей

Ансамблирование моделей – в машинном обучении техника для улучшения качества предсказаний. Основная идея заключается в том, что отдельно обучаются несколько моделей, а далее их предсказания усредняются. Давайте разберём, почему вообще это работает.

Представим, что решаем задачу регрессии, и мы обучили n-моделей, каждая из которых имеет ошибку ϵi. Будем считать, что все ошибки распределены по нормальному закону с нулевым средним: 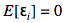дисперсией: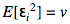и ковариацией: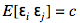

Средняя ошибка предсказаний ансамбля моделей равна следующему выражению: 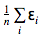Распишем математическое ожидание квадрата этой ошибки и получим следующее равенство: 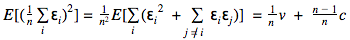Правая часть формулы позволяет сделать интересные наблюдения: – если c=v, что означает – ошибки разных моделей идеально коррелированы, то мы получим, что квадрат ошибки никак не изменится, – если c=0, когда предсказания моделей не скоррелированы, то мы получим линейное уменьшение ошибки с ростом количества моделей в ансамбле, – в промежуточных значениях, мы получаем уменьшение ошибки.

Таким образом можно сделать выводы: – ансамблирование моделей с одинаковыми ошибками не уменьшает ошибку ансамбля, – чтобы получить значительное уменьшение ошибки мы должны ансамблировать модели, в которых предсказания, а следовательно и ошибки, сильно отличаются.

Приёмы, с помощью которых можно получить модели с некоррелированными предсказаниями: – обучить модели на разных поднаборах данных, – обучить модели на разных поднаборах признаках, – обучить модели с разной начальной инициализацией параметров, – обучить разные типы моделей модели.

Данные приёмы очень активно применяются в соревнованиях по анализу данных. Таким образом, мы рассмотрели простой и эффективный способ повышения качества модели.

Есть вопрос? Напишите в комментариях!