Математика для ИИ: случайные величины и распределение вероятностей

Случайная величина — величина, случайно принимающая какое-либо значение из множества всевозможных значений. Также можно сказать, что это функция, конвертирующая результат какого-нибудь меняющегося процесса в числовое значение. Вот, как это обозначается в математике:

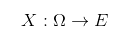
Здесь Ω — набор возможных исходов, Е — некоторое измеримое пространство. Но случайная величина — лишь шаблон и содержит возможные значения процесса. Если же мы хотим, чтобы случайная величина стала полезной по-настоящему, её надо объединить с распределением вероятностей. В результате вы узнаете, насколько каждое значение вероятно. Но так как случайные величины бывают и дискретными, и непрерывными, есть 2 способа описать распределение вероятностей.

Начнём с дискретной случайной величины. Она имеет конечное число значений, и эти значения можно рассматривать в виде категориальных переменных либо перечислений. Распределение вероятностей по такому типу случайных величин описывают функцией вероятностной массы (PMF — probability mass function). Данная функция определяет вероятность, что случайная дискретная величина равна тому либо иному значению. При этом предполагается, что Х: Ω → [0, 1] является дискретной случайной величиной, содержащей набор возможных исходов Ω для пространства со значениями 0 и 1:

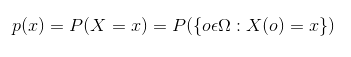
Перейдём к случайной величине непрерывного типа. Она имеет значения из множества действительных чисел (а этих чисел — бесконечное множество). Распределение вероятностей непрерывной случайной величины определяют посредством функции плотности вероятности (PDF — probability density function).

Данная функция должна чётко отвечать условиям: 1) область р есть набор всех возможных значений х (функция принимает лишь значения, которые больше либо равно 0); 2) функция должна соответствовать следующему условию:

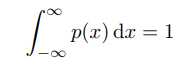
Однако проблема заключается в том, что данная функция не определяет вероятность конкретного значения, а обеспечивает вероятность нахождения данного значения в бесконечно малой области значений. На то есть причина: вероятность, что распределение вероятности получит какое-нибудь конкретное значение, равна нулю, ведь существует бесконечное множество всевозможных значений. А вероятность нахождения х где-нибудь в промежутке [a, b] определяется следующим образом:

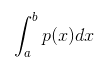
Источник: «Mathematics for Artificial Intelligence – Probability».