Метод R/S: вычисление показателя Херста

Мы уже упоминали про показатель Херста. Однако существует и иной метод его вычисления — «метод нормированного размаха». О нём и поговорим.

Для анализа временных рядов Херст предложил использовать при анализе наблюдений безразмерный показатель в виде отношения размаха (R) накопленного отклонения от среднего к среднеквадратическому отклонению (S) – (R/S)-метод.

Показатель Херста H = H(N), характеризующий фрактальную размерность рассматриваемого временного ряда, может быть получен из следующего соотношения:

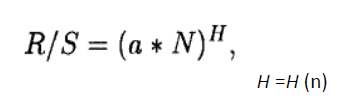
Логарифмируя обе части этого равенства и полагая значение a=1/2, получаем последовательность декартовых координат (x_n, y_n) точек Н.

Траектории ординаты yn =H(n)= log(R(n) /S(n) /log(n/2)).

Траектория абсциссы xn = n, n =3, 4, ..., m.

Требуемая для фрактального анализа ряда R/S-траектория представляется в логарифмических координатах последовательностью точек, абсциссы которых xn=log(n/2), а ординаты yn=log(R(n) /S(n)).

Соединяя отрезком соседние точки (x_n , y_n) и (x_n+1, y_n+1) , n = 3, 4, ..., m−1, получаем графическое представление R/S-траектории (Н-траектории) в логарифмических координатах (в обычных декартовых координатах).

Данный метод может быть легко применён на практике. Обладая достаточным уровнем надёжности, в то же время метод является простым в применении. Однако данный метод крайне чувствителен к длине ряда.

Для получения точных результатов оценки показателя Херста необходимо для проведения анализа несколько тысяч наблюдений в исследуемом ряду. Таким образом, в качестве недостатка данного метода можно отметить то, что R/S-метод не позволяет оценивать локальный Херст.

Хотите знать больше? Добро пожаловать на мой Телеграм-канал!