Чем хороши префиксные деревья?

Как эффективно решить задачу автодополнения для строки поиска? Точнее, какую структуру данных выбрать, чтобы хранить все известные слова, для которых потребуется искать окончания? Попробуем разобраться.

Почему массив плохо подходит?

Проверка, совпадает ли строка-паттерн, для которой мы ищем продолжение, с началом другой строки в худшем случае требует O(k) времени, где k — длина паттерна. Фильтрация всех слов в массиве, соответствующих паттерну, займёт O(nk) времени в наихудшем случае — и никак не меньше, чем O(n), где n — количество слов. Слишком медленно, слишком неэффективно.

Поможет ли ассоциативный массив?

В плане скорости обработки запроса — безусловно, да, так как хеш-таблицы, например, могут обеспечить в среднем O(1) для запроса (в случае со строками в качестве ключей всё равно может потребоваться O(k) операций, так как нужно сравнивать две строки на равенство, но количество сравнений строк будет равно O(1)). В качестве ключа использовать множество всех возможных паттернов, а в качестве ассоциированного значения — список ссылок на подходящие строки или набор возможных продолжений.

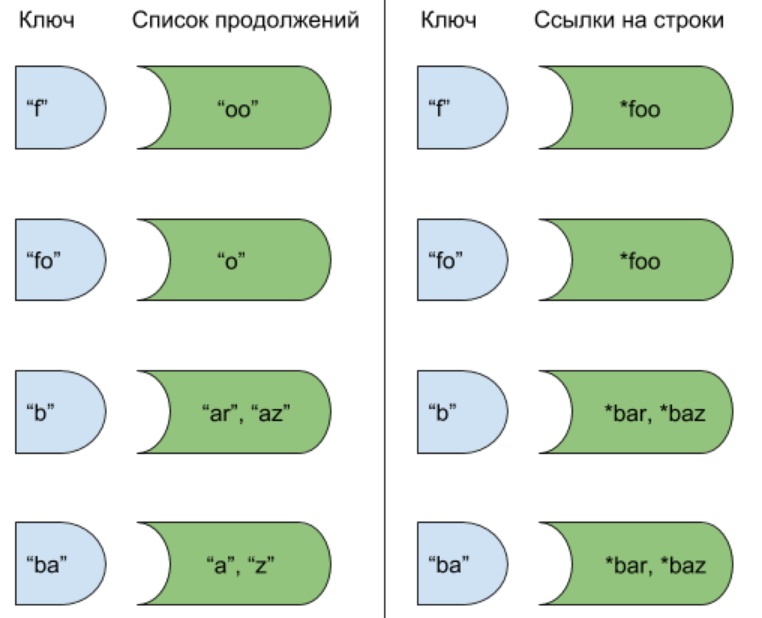Рис. 1. Так выглядит словарь для трёх слов: “foo”, “bar”, “baz” для каждого из суффиксов, подсказывающий возможные продолжения. Справа вариант, хранящий строки-продолжения, слева — хранящий ссылки на возможные продолжения.

И хотя ассоциативный массив гораздо лучше, чем обычный массив или список, он всё же не оптимально распоряжается ресурсами: каждый ключ — это один из возможных префиксов, и некоторые префиксы могут быть вложены друг в друга, как матрешка (“f” и “foo”, “b” и “ba”): это можно использовать для оптимизации хранения данных.

Trie

Определение Trie (или бора, или префиксного дерева) довольно простое:

#include <unordered_map>  // обеспечивает поиск за O(1)

struct Trie {
    int isLeaf;
    std::unordered_map<char, Trie> children;
};

Каждый узел хранит коллекцию ссылок на дочерние узлы (фактически, другие Trie). Проходя от корня до узла, можно получить префикс, ассоциирующийся с этим узлом. Обычно в узлах Trie не хранятся ключи (но, естественно, структуру данных можно расширить и хранить в узлах, что душа пожелает, например, ассоциированные с ключами значения). Однако ключ можно «восстановить», пройдя от корня до одной из листовых вершин (помечена как isLeaf). Если соответствующей ключу листовой вершины нет в Trie, значит, такой ключ здесь не хранится.

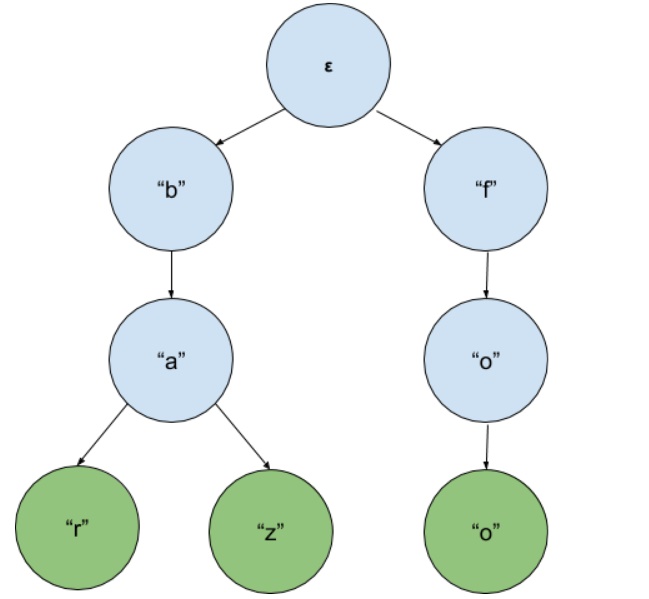Рис. 2. Пример Trie, сформированный из строк “foo”, “bar”, “baz”. Зелёным выделены листовые вершины. В корне находится ε — символ, обозначающий пустую строку.

Чтобы использовать Trie для автодополнения, нужно взять строку-паттерн и найти узел в дереве, соответствующий этой строке (если такого узла нет — значит, известных продолжений строки нет). Все возможные листья найденного узла и есть строки-кандидаты для автодополнения!

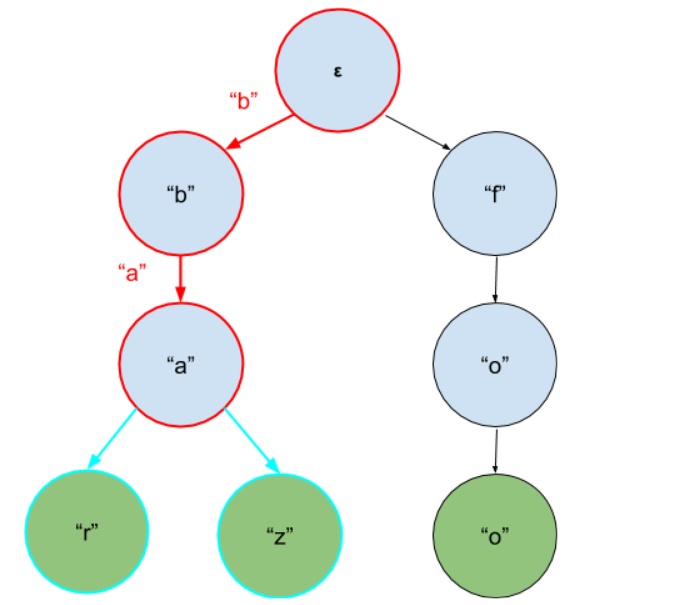Рис. 3. Поиск всех известных продолжений строки “ba” в Trie. Красным выделен путь, который пройден от корня до узла, соответствующего “ba”, бирюзовым — возможные продолжения (“r” и “z”). Глубина продолжений может быть больше одного уровня.

Время на поиск нужного узла — O(k), где k — длина строки, так как надо сделать максимум k-операций по поиску нужной ссылки в k-узлах.

Как и поиск, вставка и удаление элементов из Trie требуют O(k) операций, что позволяет эффективно расширять или чистить словарь.

На практике для автодополнения используют более эффективные DAFSA, которые расширяют и дополняют идею Trie.

Как ещё использовать Trie

Также Trie можно использовать как быстрый ассоциативный массив для хранения ключей, которые можно представить как последовательности — не только строки, но и массивы, списки и так далее.

Легко обеспечить обход всех листьев Trie (точнее, ассоциированных с ними ключей) в отсортированном порядке. Поскольку алфавит (или набор возможных элементов в последовательностях) ограничен, то отдельный уровень Trie можно сортировать за линейное время относительно количества дочерних узлов и размера алфавита O(n + K) при помощи алгоритма сортировки подсчетом (Counting Sort). Более подробно сортировка при помощи Trie за O(N) рассматривается здесь и на странице обсуждения статьи или здесь — см. раздел «Tries».

Вариант Trie, хранящий в узлах ссылки на другие узлы, используется в качестве основы для алгоритма Ахо-Корасик, который ищет все вхождения набора строк в текст за линейное время (он используется в утилите fgrep).

При помощи Trie можно легко подсчитать количество значений, если данные являются иерархическими: например, количество номеров телефонов, начинающихся с +7(900) …, или количество почтовых индексов в одном регионе, и так далее — если в каждом узле сохранять количество его вхождений.

Также есть усовершенствования Trie, направленные на дальнейшее «сжатие», например, компактное префиксное дерево (Radix Tree, или PATRICIA).

Множество применений Trie нашло в области, где часто приходится работать с текстовыми последовательностями — биоинформатике. В общем, это довольно простая, но гибкая и эффективная структура данных, которая может быть полезной для решения самых разных задач.