Как бороться с мультиколлинеарностью?

Как известно, уменьшение размерности применяется в машинном обучении в двух целях: для визуализации (чтобы данные с большим количеством признаков можно было отобразить в двух- или трёхмерном пространстве) и для уменьшения количества переменных.

Второе применение является более фундаментальным, базовым и основным. Здесь уместно вспомнить курс школьной математики, а точнее, систему уравнений, в которой переменных было больше, чем самих уравнений. И решить его в школьные годы мы, разумеется, не могли.

Похожую аналогию можно провести и с задачами по Machine Learning, когда в количественном отношении данных меньше, чем признаков. Обучить такую модель достаточно сложно, да и хорошо работать она, скорее всего, не будет. Вдобавок ко всему, при увеличении размерности задачи данные приобретают сложно анализируемый для модели характер.

Продолжая говорить о базовых вещах, нельзя не вспомнить о понятии мультиколлинеарности. Когда в матрице признаков какие-то признаки являются линейной комбинацией друг друга — это называется сильной коллинеарностью (грубо говоря, можно выразить один признак через другой), а когда речь идёт о сильной корреляции — это слабая или частичная коллинеарность, что тоже плохо. Такая задача решается очень неустойчиво.

Как бороться с мультиколлинеарностью?

Один из подходов — уменьшить размерность, но не просто выкинуть переменные, а перейти к другим переменным. Другой подход борьбы с мультиколлинеарностью — всем известная регуляризация:

L1 — lasso regression: 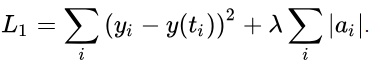L2 — ridge regression: 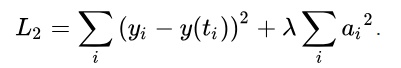Штрафуя модель, мы ограничиваем то количество решений, которое в случае с мультиколлинеарностью слишком велико или бесконечно, некоторым набором решений. Да, в результате мы получаем несколько смещённую оценку, но она смещена не сильно. Таким образом от глобальной проблемы (задачу решить в принципе нельзя) мы переходим к конкретному результату, когда задача решена не самым оптимальным способом, но, тем не менее, устойчивое решение мы нашли.

Вообще, можно показывать очень интересные вещи с матричными фокусами, однако об этом пойдёт разговор в лекции про сингулярное разложение SVD. Если не хотите её пропустить, записывайтесь на курс «Data Scientist» в OTUS!

Есть вопрос? Напишите в комментариях!