Доверяй, но проверяй: почему нужно проводить А/B-тестирование

«Матемаркетинг» — конференция по маркетинговой аналитике. В этом году Think with Google Russia — её информационный партнёр. Среди главных тем «Матемаркетинга»: анализ данных в digital-маркетинге, алгоритмический маркетинг и оптимизация маркетинговых задач. В прошлом году мне приходилось выступать на этой конференции в качестве Head of Data Science из Х5 Retail Group с докладом о методах А/B-тестирования. В этой статье представлены подробности выступления.

Базовое А/B-тестирование

А/B-тестирование проводят, чтобы понять, как какое-то изменение на сайте, в магазине или в приложении повлияет на результат.

Как это работает? Есть две группы покупателей или клиентов, похожих друг на друга почти по всем параметрам. Временной промежуток — один и тот же, как и поведение пользователей, разница лишь в целевом воздействии. Если после него статистические метрики групп отличаются, значит на показатели повлияли именно внесённые изменения.

Но бывают и другие случаи. Например, однажды перед Х5 встала задача оценить, насколько Чемпионат мира по футболу повлиял на продажи пива. Чтобы сравнить результаты, нужны две параллельные вселенные. В одной из них проходил Чемпионат мира, а в другой — нет. Но если сравнивать настоящую вселенную не с чем, то нужно использовать другие способы.

Методология тройной разности

Смысл метода в том, чтобы сначала сравнить результаты между двумя временными точками (между 1 сентября и 1 октября, например) за один год, а потом сделать то же самое для предыдущего года. Конечный шаг — найти разность между полученными величинами.

Это довольно простой, но далеко не самый точный метод.

Байесовский структурный временной ряд

Воображаемая ситуация: в России только что прошёл Чемпионат мира по футболу. Сеть розничных магазинов хочет проверить, чем вызван рост продаж пива в Москве — наплывом болельщиков или другими факторами. Чтобы предсказать начальную вероятность, строят временной ряд из имеющихся данных: это могут быть клики от рекламы или результаты продаж. Затем ищут город с такими же показателями, но где чемпионат не проходил. Например, Челябинск. Это будет второй, коррелирующий временной ряд. На его основе выстраивают модель пространства состояния (State-Space model) и выдвигают ещё один прогноз. Если связать его с первоначальным, получится такое изображение:

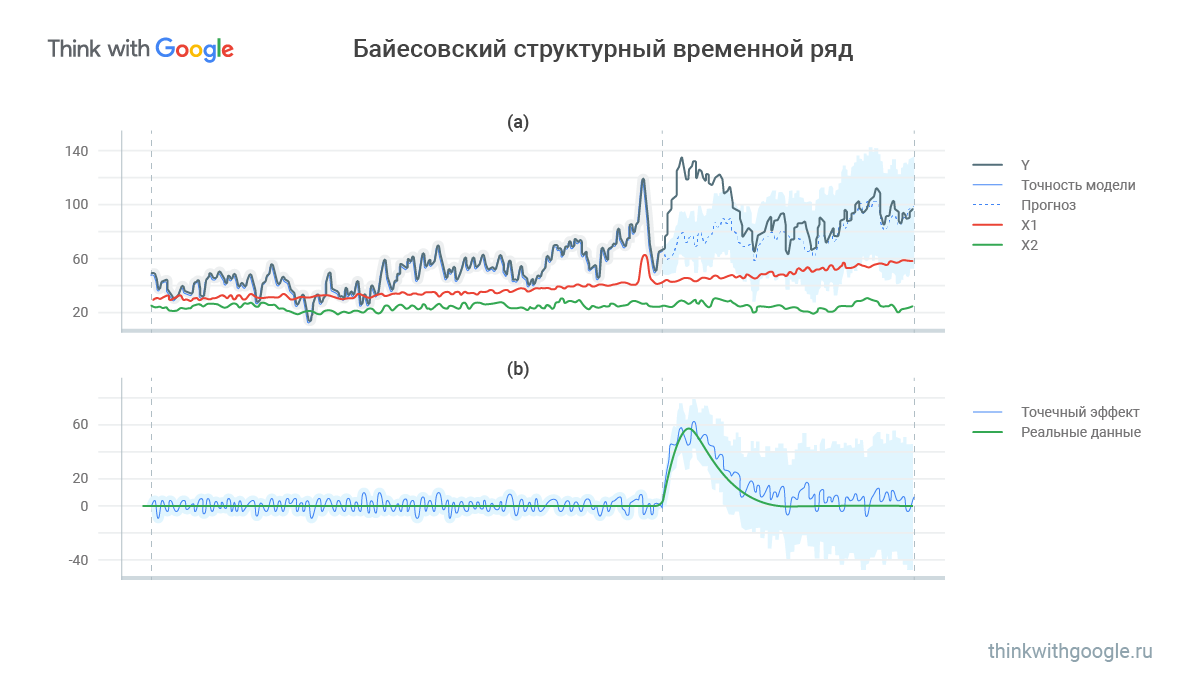
В (а) синяя линия — спрогнозированные значения; Х1 и Х2 — коррелирующие ряды; черная линия — то, что произошло по факту. В какой-то момент заметен серьезный разрыв между реальностью и предсказанными результатами. Чтобы устранить разницу, производится воздействие — например, с определенного момента все показатели умножают на 1,1. На графике (b) зелёная линия соответствует реальному эффекту, а синяя — предполагаемому. В итоге отличие реального от предсказанного — и есть эффект.

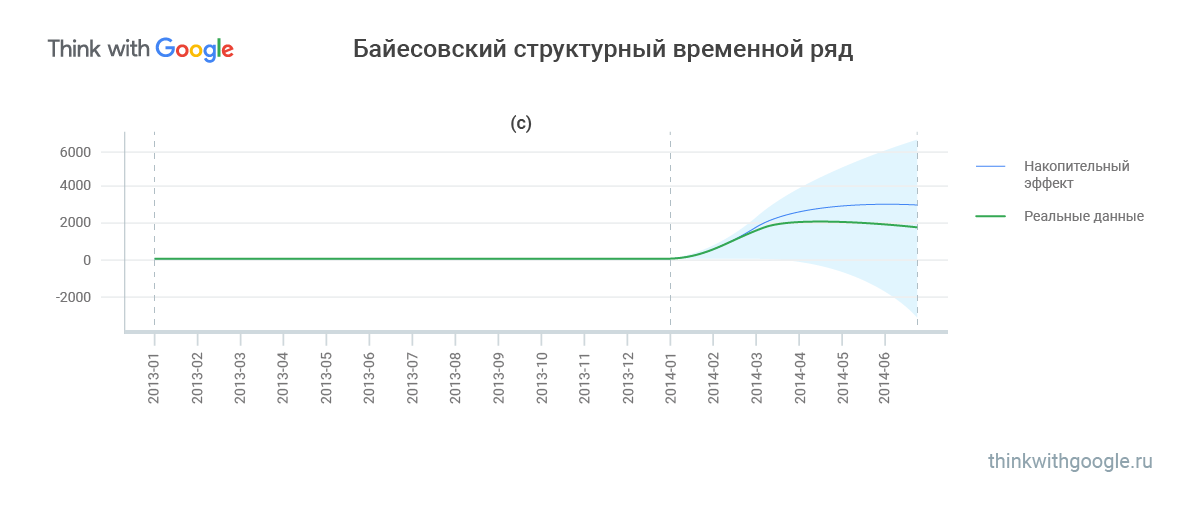
В (с) видно, как кумулятивное воздействие почти совпадает с тем, что было на самом деле.

Регрессионный анализ

Пример: ритейлер хочет оценить эффект от новой раскладки товаров в магазине, чтобы узнать, вырастут ли продажи. Чтобы сделать это, нужно учесть продажи смежных товаров, сравнить их с предыдущими продажами «нашего» товара и выстроить модель, по которой можно будет делать прогнозы.

Чтобы понять, что повлияло на сегодняшние продажи, нужно построить объяснительную модель. Предположим, она имеет нормальное распределение ошибок. Если это так, то все значимые факторы учтены.

Для контрольных магазинов можно вычесть из реальных дневных продаж (красная прерывистая линия) дневные продажи, предсказанные моделью (зелёная прерывистая). Так получают нормальное распределение ошибок с центром в нуле. В них ничего не менялось, и модель будет приблизительно совпадать с реальностью. Для магазинов из тестовой группы нужно вычесть из реальных дневных продаж (синяя сплошная линия) модельные дневные продажи (зелёная прерывистая) и так же получить нормальное распределение. Тогда, если ничего не изменилось, центр будет где-то около нуля; если продажи улучшились, будет смещен вправо, если ухудшились — влево.

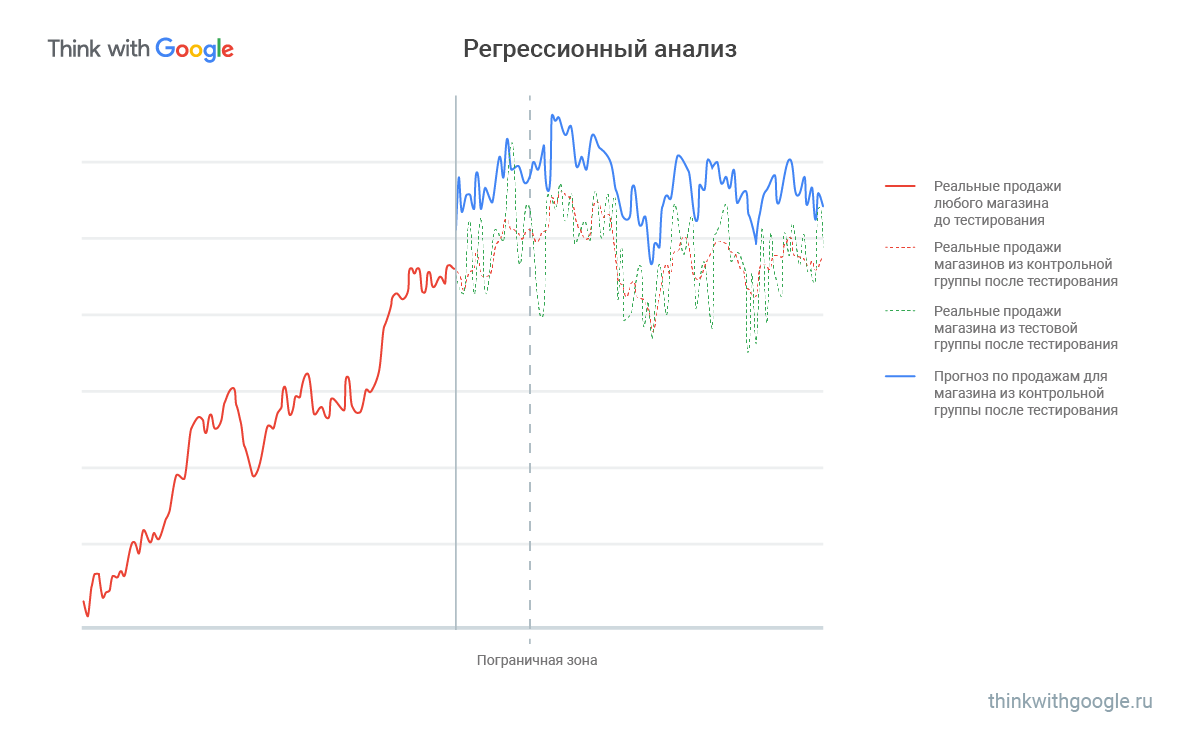
На основе данных о продажах смежных товаров можно спрогнозировать, как продаётся нужный нам товар. Если есть какие-то внешние причины, почему продажи изменились (государственный выходной, оцепление района, ремонт дороги), продажи смежных товаров в модели тоже будут падать, то есть ошибка не сместится. Чтобы учесть эту особенность, нужно построить модель распределения ошибки для контрольной группы и для тестовой, а потом сравнить их. Это поможет сделать вывод о том, как изменение повлияло на продажи.

В чём ещё плюс таких симуляций? Так можно понять, насколько данные чувствительны к изменениям: например, умножить показатели на 1,01 и посмотреть, сдвинулись ли они.

Выводы и нюансы:

• если нет возможности поделить аудиторию/клиентов на две группы, это ещё не означает, что А/B-тестирование невозможно. Помимо базового, есть ещё много других методов, их выбор зависит от задачи; • при любом А/B-тестировании нужно учитывать эффект новизны. Когда изменения только появились, продажи могут расти. Это не всегда говорит о положительном влиянии самих обновлений. Покупатели видят, к примеру, новую раскладку товаров, и интерес вызывает у них желание что-то купить. Поэтому в любом А/B-тестировании анализировать результаты нужно после первой недели. Чаще всего именно тогда эффект новизны сходит на нет.

Особая благодарность за материалы по второму методу Павлу Нестерову.