LogSumExp трюк

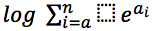Очень часто в задачах машинного обучения у нас следующая задача. Дан массив чисел: Надо посчитать величину: Необходимость подсчёта такого выражения возникает например в EM-алгоритме на E-шаге, когда мы считаем апостериорное распределение на скрытые переменные. А числа представляют логарифм от плотности вероятности и являются большими по модулю отрицательными значениями.

Если мы попробуем взять экспоненту большего по модулю отрицательного значения, то ввиду ограниченной точности вычислений на компьютерах мы получим ответ равный нулю. Таким образом, в нашем исходном выражении мы можем получить ноль под знаком логарифма и ошибку при вычислении или некорректный ответ.

Например:

import numpy as np

a = np.array([-1000, -2000, -2000])
print(np.log(np.sum(np.exp(a))))
>>> -inf

Существует достаточно простой и элегантный способ обойти эту проблему

Обозначим 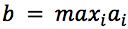и запишем искомое выражение: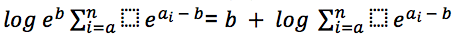Заметим, что в правой части под знаком логарифма уже никак не может стоять ноль, так как по крайней мере одно слагаемое суммы равно 1, и мы можем корректно посчитать данное выражение.

Данная функция реализована, например в пакете scipy:

import numpy as np
from scipy.misc import logsumexp

a = np.array([-1000, -2000, -2000])
b = a.max()
print(b  + np.log(np.sum(np.exp(a - b)))
>>> -1000

print(logsumexp(a))
>>> -1000

Так мы рассмотрели очень простой, но эффективный способ для обхода ошибок округления, которые возникают в задачах машинного обучения.