Расстояние Вассерштейна: WGAN и 2 кучи земли

В январе 2017 года команда из Курантовского института математических наук и Facebook AI Research выложила в открытый доступ препринт статьи под названием «Wasserstein GAN».

Основное отличие этой статьи от большинства публикаций предлагающих очередное улучшение для Генеративных Состязательных Сетей заключается в фундаментальной теоретической базе. Авторы не просто демонстрируют очередной набор удачных изображений, порождённых GAN’ами, но и объясняют эффективность данного подхода с точки зрения теории. И в центре этой теории как раз и лежит расстояние Вассерштейна.

Если подробно разобрать оригинальную статью, то окажется, что в базовой версии GANs минимизируется дивергенция Дженсена-Шеннона, которая является суммой двух дивергенций Кльбака-Лейблера. Оба этих страшных словосочетания обозначают некоторые меры близости для пары распределений. Если вы хорошо знакомы с теорией информации, то вам будет не слишком сложно придумать два распределения, для которых эти меры будут бесконечными, что, конечно же, будет сильно препятствовать сходимости любого алгоритма машинного обучения.

Для таких как я, замечу

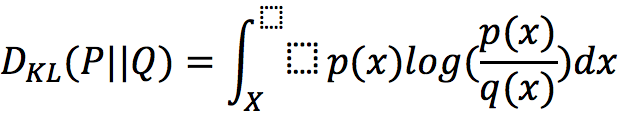В этой формуле наличия одной такой точки «x», в которой q(x)=0, а p(x)>0, достаточно для того, чтобы интеграл разошёлся. Но как нам с этим поможет широко известный в узких кругах выпускник МГУ Леонид Вассерштейн?

Давайте разберёмся

Определение расстояния Вассерштейна довольно громоздко и, по правде, мне тоже непонятно: 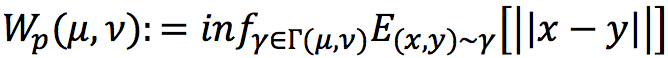К счастью, есть простая и наглядная интерпретация. Допустим, заданы две функции плотности распределения 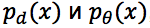Где «d» – обозначает data или данные, а «θ» – параметры нейронной сети, раз уж мы говорим о них. 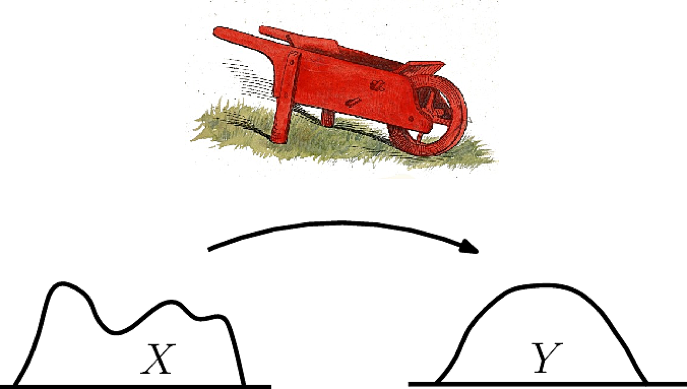Изображение взято с сайта Structural Bioinformatics Library

Можно представить, что это две кучи земли. Обе содержат одинаковое количество земли, так как по определению их интегралы равны единице и мы хотим одну кучу переместить так, чтобы образовалась другая. При этом «стоимость» перемещения земли равна произведению перемещаемой «массы» на расстояние.

Хочется заметить, что используя такую интерпретацию, разобраться с формулой не составляет большого труда. Не буду вдаваться в детали, понятно, что для любых двух распределений, «стоимость» переноса должна оказаться конечной, то есть для любого изменения параметров theta мы можем сказать, стало ли расстояние Вассерштейна меньше.

Конечно, вычисление точного расстояния между распределениями, как это часто бывает, оказывается невозможным. Однако авторы показывают, что мы можем минимизировать мажорирующее распределение, чего, конечно же, достаточно.

Итог

В заключение остается только привести примеры изображений, порождённых сетями GAN и WGAN:

Эти изображения взяты из статьи Wasserstein GAN. В качестве обучающей выборки использовался датасет с соревнования Large-scale Scene Understanding Challenge. Левая плашка содержит изображения, сгенерированные моделью, использующей расстояние Вассерштейна, а правая – оригинальную функцию потерь GANs.

В следующий раз я собираюсь рассказать о том, как можно вывернуть GAN наизнанку и почему так надо делать.

Есть вопросы? Напишите в комментариях!