Передача сообщений по нейросети
В предыдущем посте я рассказал о том, как делать свёртки на графах. Одним из ключевых моментов было понятие сообщения, которое задавалось как:
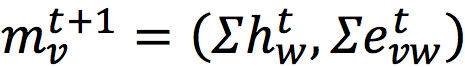Из-за того, что внутри вектора сообщения происходит независимое суммирование состояний соседних вершин и состояний рёбер, итоговая модель не может учитывать корреляции между вершинами и её рёбрами. Фактически нам бы хотелось, чтобы каждая соседняя вершина независимо от других передавала своё сообщение на очередном шаге. 
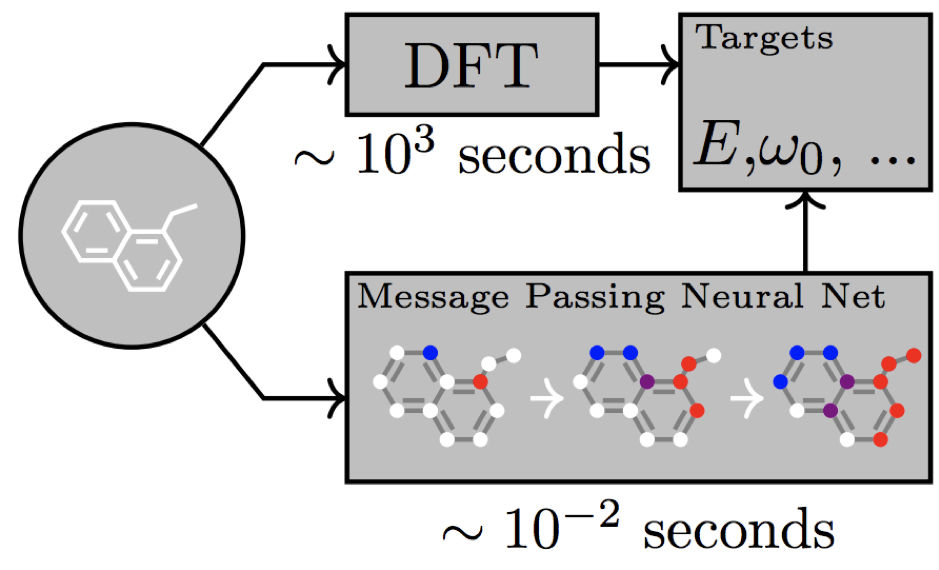В статье 2017 года Neural Message Passing for Quantum Chemistry от команды Google Brain было предложено обобщение свёртков на графах под названием Message Passing Neural Networks (MPNN). Сообщение получаемой вершиной предлагалось вычислять по следующей формуле:
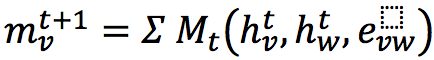Суммирование снова происходит по всем соседним с «v» вершинам, «Mt» — функция сообщения, зависящая не только от состояния соседней вершины и ребра до текущей, но и от состояния текущей вершины.
Эта функция может быть произвольной дифференцируемой функцией с обучаемыми параметрами, например, нейронной сетью. К тому же, нетрудно заметить, что в случае
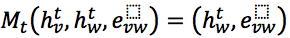мы получаем сообщение аналогичное предыдущему. Точно так же как и в предыдущем посте мы задаём функцию обновления состояния вершины:
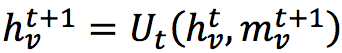Которая тоже может быть представлена нейросетью. И в конце концов мы хотим получить итоговый вектор с помощью ещё одной функции R:
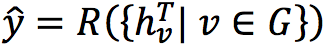В этот раз к выходной функции есть дополнительное требование — она должна быть инвариантна к порядку вершин, то есть, по сути, она должна принимать на вход множество вершин, а не их список. Благодаря этому требованию весь алгоритм MPNN оказывается инвариантным к графовому изоморфизму, поскольку каждая из функций M, U и R является таковой.
Стоит добавить, что хотя работа команды из Google Brain была не первой в этом направлении, они смогли обобщить большое количество работ предшественников и при этом показали потрясающие результаты в решаемой задаче. В частности, они обучили свою модель решать задачу предсказания квантовохимических свойств молекул и сравнили скорость с классическими методами квантового моделирования, получив в результате увеличение скорости на 5 порядков! И это при лучшей точности по сравнению с другими публикациями в этой области.
Остались вопросы? Напишите в комментариях!
