Свёрточные сети на графах
Давайте рассмотрим свёрточные сети, но не обычные свёртки, а скорее их аналог для работы с графовыми данными. Граф — это сложный и непонятный для привычных нам нейронных сетей объект. Самый простой способ представить граф для работы с ним — записать его в виде матрицы смежности, в которой каждой вершине соответствует своя строка и свой столбец. В простейшем виде, такая матрица будет содержать только рёбра — единицы в клетках пересечения строк и столбцов, соответствующих связанным вершинам.
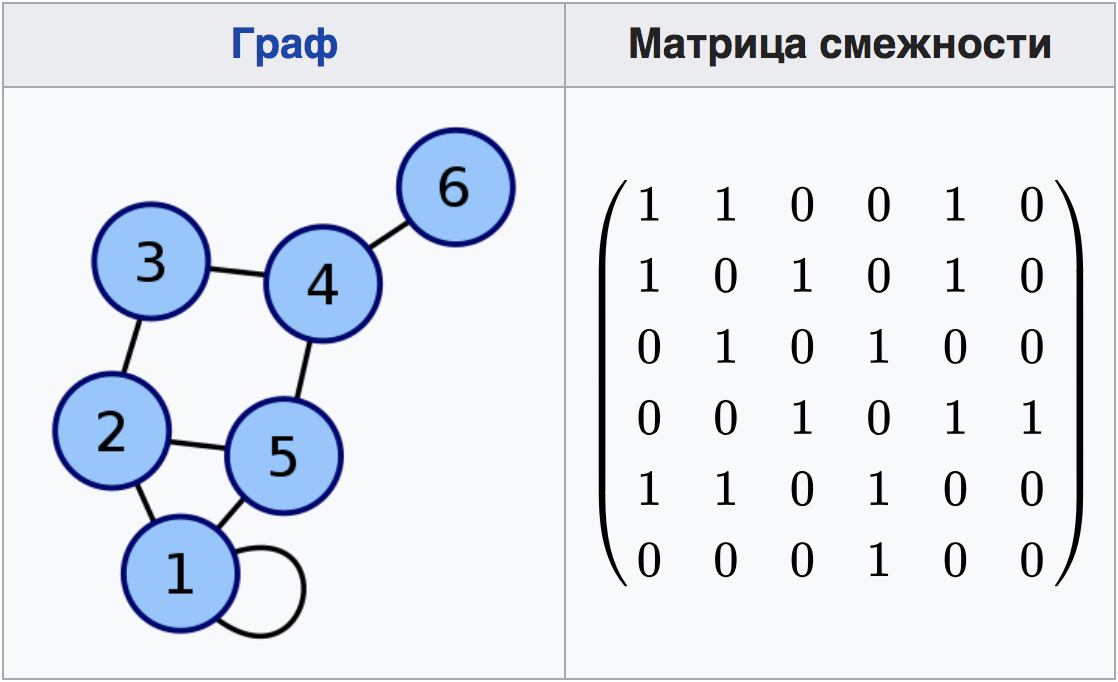
Однако мы можем захотеть хранить больше информации в этой матрице. Тогда, например, на диагонали будут находиться состояния вершин, а в клетках рёбер состояние рёбер. Кроме того, эти самые состояния не обязательно представляют из себя одно единственное число: рёбра могут иметь направления и т.д.
В 2015 году учёные из Гарвардского Университета предложили новый подход для работы с графами — Свёрточные сети на графах (Convolutional Networks on Graphs). Решая задачу об извлечении признаков из графового представления молекул, они предложили следующий подход.
Пусть
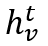состояние вершины «v» в момент времени «t». Аналогично,
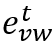— состояние ребра между вершинами «v» и «w» в момент времени «t». Тогда назовём сообщением:
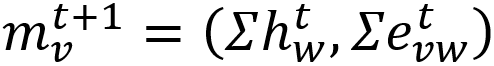В этой формуле обе суммы берутся по всем w соседним с v, а скобки обозначают конкатенацию векторов. Вычислив для каждой вершины её сообщение, мы теперь можем обновить её состояние:
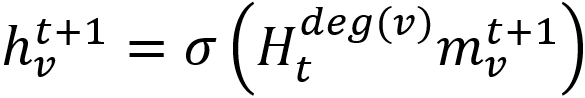где
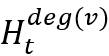— своя матрица параметров для каждого временного шага и для каждой степени вершины 𝑑𝑒𝑔(𝑣). После нескольких таких шагов вычисляется функция от всего графа:
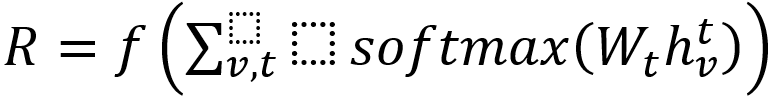где f — нейронная сеть, а Wt — матрица «выходных» весов, своя для каждого временного шага.
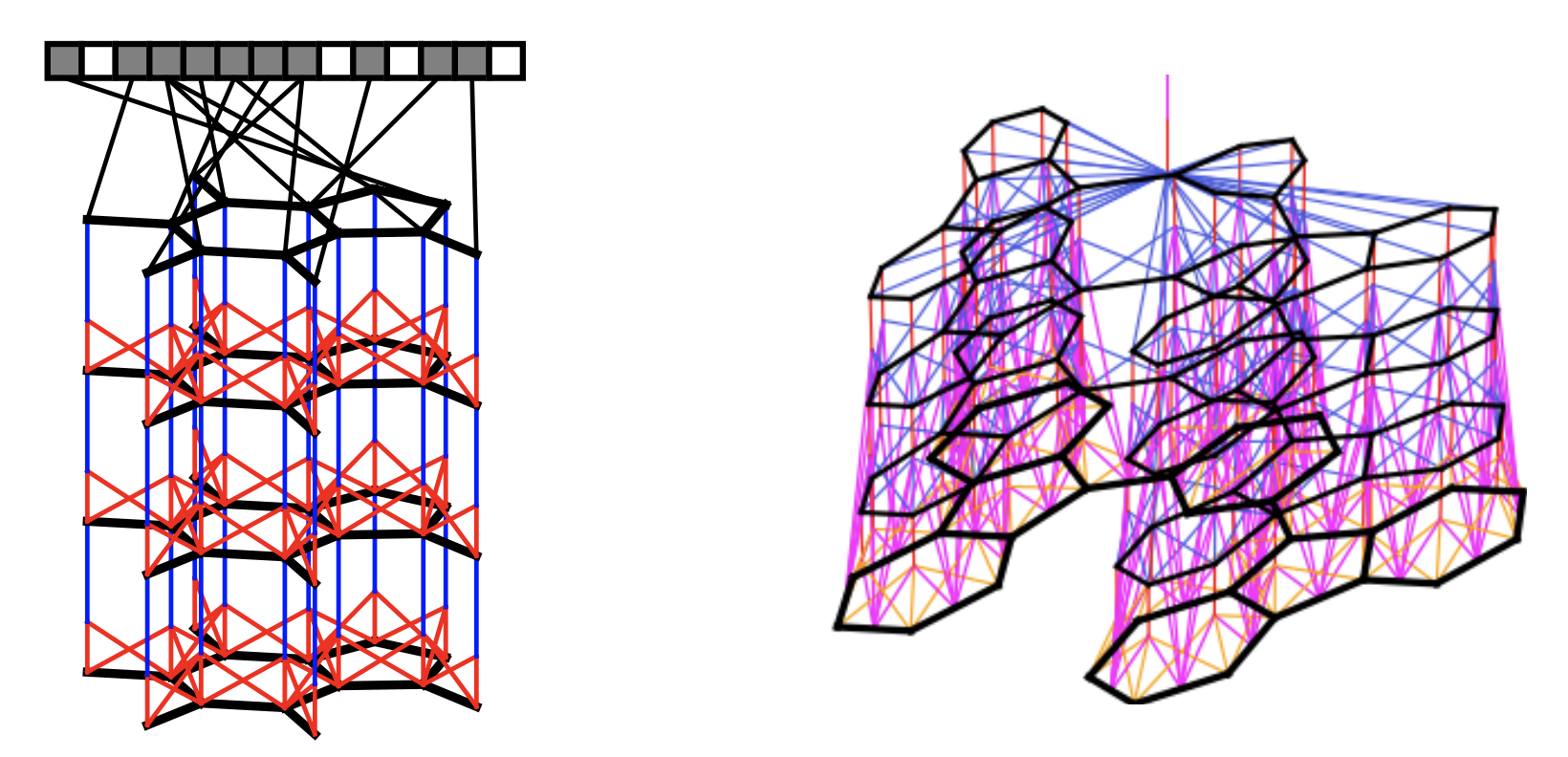До этого момента мы никак не коснулись того, почему же такая модель получила название «свёрточной». Но на самом деле, если произвольное изображение вы представите в виде графа, каждая вершина которого соответствует пикселю, её состояние — просто цвет, а рёбра будут только между соседними пикселями, то станет понятно, что свёртки на графах — простое обобщение классических свёрточных сетей.
Такой подход имеет свои плюсы и минусы, и, безусловно, за три прошедших года в работе с графами всё сильно изменилось.
Есть вопросы? Напишите в комментариях!
