Математика для ИИ: нормы

В некоторых случаях при работе с вектором необходимо знать размер вектора. В таких ситуациях помогают специальные функции, называемые нормами — Lⁿ.

Что означает маленькая буква n? Это число измерений, в которых находится вектор. С учётом того, сколько конкретно измерений существует в вашем векторном пространстве, будут различаться и нормы. Самая известная норма — норма 2-мерного пространства (её ещё называют Евклидовой). Очень часто она представляет собой Евклидово расстояние от начала вектора до точки в пространстве, которая находится на конце данного вектора. В случае обобщения пространства на несколько измерений применяют глобальную норму:

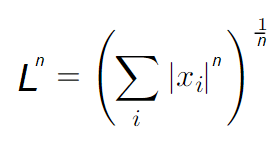
В принципе, нормой может быть, по сути, любая функция, которая удовлетворяет ряду требований:

Нередко, когда разработчик создаёт ИИ-приложение, важным является различить элементы, которые равны 0, и элементы, значение которых близко к 0, но нулём не является. В этих случаях применяют норму L¹. Это простая норма, которая растёт с одинаковой скоростью в любых точках векторного пространства. Когда любой элемент вектора x передвигается от 0 к a, то функция ниже вырастает на a:

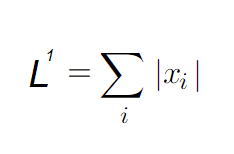
Как известно, в глубоком обучении параметры нейросетей абстрагируются как матрицы. В результате нам необходимо знать размер матрицы, а здесь очень поможет норма Фробениуса:

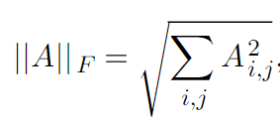
Источник — «Mathematics for Artificial Intelligence – Linear Algebra»