Методы сортировки данных. Алгоритмы поиска и сортировки
Алгоритмы сортировки данных широко используются в программировании для решения различных задач. В этой статье мы рассмотрим несколько основных алгоритмов сортировки данных в массиве.
Для начала давайте вспомним, что массив — это структура данных, которая хранит набор значений. Компоненты массива идентифицируются по индексу либо набору индексов, которые принимают целые значения из некоторого непрерывного заданного диапазона.
Но прежде чем идти дальше и говорить про алгоритмы сортировки, давайте вспомним про метод
void Swap(T[] items, int left, int right) { if (left != right) { T temp = items[left]; items[left] = items[right]; items[right] = temp; } }
Что же, теперь можно приступать и к рассмотрению алгоритмов сортировки. Начнём с пузырьковой.
Пузырьковая сортировка данных
Сортировка пузырьком считается самым простым алгоритмом сортировки. В данном случае алгоритм проходит по массиву несколько раз, причём на каждом этапе происходит перемещение в конец массива самого большого из неотсортированных значений.
Представим, что у нас есть массив целых чисел:

Во время первого прохода по массиву сравниваются значения 3 и 7. Так как семь больше, всё остаётся в первоначальном виде. Далее сравниваются 7 и 4. Т. к. четыре меньше, цифры меняются местами:

В общем, процесс повторяется, пока 7 не дойдёт практически до конца. Почему практически? Потому что, как вы уже наверняка догадались, последний элемент — это 8, который больше семи, поэтому обмен не происходит. Всё чрезвычайно просто:

Однако пока обмен происходит, сортировка продолжается, в результате чего перемещается 6:

При очередном проходе обмен не выполняется, т. к. все значения массива расположены по порядку. В итоге алгоритм сортировки пузырьком заканчивает свою работу.
public void Sort(T[] items) { bool swapped; do { swapped = false; for (int i = 1; i < items.Length; i++) { if (items[i - 1].CompareTo(items[i]) > 0) { Swap(items, i - 1, i); swapped = true; } } } while (swapped != false); }
Сортировка данных вставками
Эта сортировка работает путём прохождения по массиву и перемещения нужного значения в его начало. Важно помнить, что сортировка обрабатывает элементы массива по порядку. Т. к. алгоритм работает слева направо, становится очевидно, что всё, что находится слева от текущего индекса, — отсортировано. Давайте посмотрим на увеличение отсортированной части массива с каждым последующим проходом:
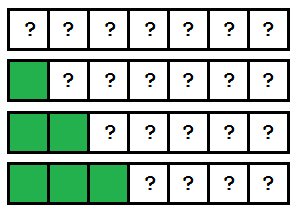
По ходу работы отсортированная часть массива растёт, таким образом, в конечном итоге, массив становится упорядоченным.
Приведём пример. Вот неотсортированный массив:

Алгоритм сортировки начнёт работать с индекса «ноль» и значения «три». Т. к. это 1-й индекс, массив до него включительно будет считаться уже отсортированным.
Потом перейдём к семёрке. Семь больше любого значения в отсортированной части, значит, осуществляется переход к последующему элементу. Отметим, что на прошедшем этапе были отсортированы компоненты с индексами 0..1, про компоненты с индексами 2..n мы пока ничего не знаем.
Теперь алгоритм проверяет четвёрку. Четыре меньше, чем 7, поэтому переносится на другую, более правильную позицию, которая находится в отсортированной части массива. Позиция определяется методом
Так для вставки был определён индекс 1. Вставка осуществляется методом

Итог работы алгоритма сортировки вставками очевиден:

public void Sort(T[] items) { int sortedRangeEndIndex = 1; while (sortedRangeEndIndex < items.Length) { if (items[sortedRangeEndIndex].CompareTo(items[sortedRangeEndIndex - 1]) < 0) { int insertIndex = FindInsertionIndex(items, items[sortedRangeEndIndex]); Insert(items, insertIndex, sortedRangeEndIndex); } sortedRangeEndIndex++; } } private int FindInsertionIndex(T[] items, T valueToInsert) { for (int index = 0; index < items.Length; index++) { if (items[index].CompareTo(valueToInsert) > 0) { return index; } } throw new InvalidOperationException("The insertion index was not found"); } private void Insert(T[] itemArray, int indexInsertingAt, int indexInsertingFrom) { // itemArray = 0 1 2 4 5 6 3 7 // insertingAt = 3 // insertingFrom = 6 // // Действия: // 1: Сохраняем текущий индекс в temp // 2: Меняем indexInsertingAt на indexInsertingFrom // 3: Меняем indexInsertingAt на indexInsertingFrom в позиции +1 // Сдвигаем элементы влево на один. // 4: Записываем temp на позицию в массиве + 1. // Шаг 1. T temp = itemArray[indexInsertingAt]; // Шаг 2. itemArray[indexInsertingAt] = itemArray[indexInsertingFrom]; // Шаг 3. for (int current = indexInsertingFrom; current > indexInsertingAt; current--) { itemArray[current] = itemArray[current - 1]; } // Шаг 4. itemArray[indexInsertingAt + 1] = temp; }
Сортировка данных выбором
Сортировка выбором — некий гибрид между сортировкой вставками и пузырьковой сортировкой. Давайте посмотрим, как работает эта сортировка на нашем массиве:

Во время первого же прохода алгоритм посредством метода
Так как в нашем примере массив небольшой, мы легко скажем, что это «три», да и вообще, эта цифра уже находится там, где надо. После второго прохода мы получим следующее:

И ещё после 2-х проходов алгоритм сортировки завершит работу:

public void Sort(T[] items) { int sortedRangeEnd = 0; while (sortedRangeEnd < items.Length) { int nextIndex = FindIndexOfSmallestFromIndex(items, sortedRangeEnd); Swap(items, sortedRangeEnd, nextIndex); sortedRangeEnd++; } } private int FindIndexOfSmallestFromIndex(T[] items, int sortedRangeEnd) { T currentSmallest = items[sortedRangeEnd]; int currentSmallestIndex = sortedRangeEnd; for (int i = sortedRangeEnd + 1; i < items.Length; i++) { if (currentSmallest.CompareTo(items[i]) > 0) { currentSmallest = items[i]; currentSmallestIndex = i; } } return currentSmallestIndex; }
Сортировка данных слиянием
Предыдущее алгоритмы — линейные (имея квадратичную сложность, они используют мало памяти). Сортировка слиянием соответствует принципу «Divide and conquer» («разделяй и властвуй»). Она работает путём разделения крупной задачи на более мелкие, которые решаются проще.
Отвлечёмся на минутку
Представьте, что вы работаете на крыше или стройплощадке, и у вас повредился электрокабель, от которого запитывается важный инструмент. Строительные и кровельные кабели очень длинные и часто достигают 100 и более метров. Вам нужно срочно окончить работу, но у вас нет средств диагностики, чтобы починить провод. Неопытные работники просто прекращают все действия, доложив начальству. Мастера-сдельщики режут кабель пополам, получая в 99 % случаев 50 метров работающего провода. Если нужно, они режут пополам и неработающую часть, что позволяет либо достаточно быстро найти место внешнего повреждения, внимательно изучив четверть кабеля (25 м), либо получить в итоге 75 метров, которых хватит для выполнения большинства строительных задач. Всё, что потребуется, — нож и моток изоленты.
Пример достаточно отдалённый, но всё же помогает понять, что такое сортировка слиянием. При выполнении этого алгоритма массив делится пополам до тех пор, пока каждый участок не будет иметь длину в один элемент. Далее участки сливаются (возвращаются на место), но уже в правильном порядке.
Итак, наш массив:
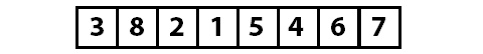
Он делится наполовину:

И потом опять, и опять наполовину:

Потом сливание/соединение в верном порядке:

И результат:
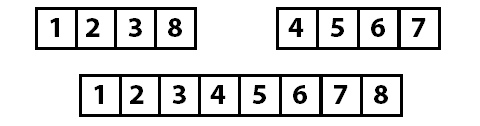
Алгоритм работает путём реализации следующих операций:
1. Рекурсивное разделение массива на группы с помощью метода
Сортировка слиянием делит и склеивает массив вне зависимости от того, был ли он изначально отсортирован либо нет. Это значит, что данный алгоритм — не самое оптимальное решение, если наш массив уже частично упорядочен и отсортирован (производительность сортировки слиянием может быть ниже, чем у линейного алгоритма).
public void Sort(T[] items) { if (items.Length <= 1) { return; } int leftSize = items.Length / 2; int rightSize = items.Length - leftSize; T[] left = new T[leftSize]; T[] right = new T[rightSize]; Array.Copy(items, 0, left, 0, leftSize); Array.Copy(items, leftSize, right, 0, rightSize); Sort(left); Sort(right); Merge(items, left, right); } private void Merge(T[] items, T[] left, T[] right) { int leftIndex = 0; int rightIndex = 0; int targetIndex = 0; int remaining = left.Length + right.Length; while(remaining > 0) { if (leftIndex >= left.Length) { items[targetIndex] = right[rightIndex++]; } else if (rightIndex >= right.Length) { items[targetIndex] = left[leftIndex++]; } else if (left[leftIndex].CompareTo(right[rightIndex]) < 0) { items[targetIndex] = left[leftIndex++]; } else { items[targetIndex] = right[rightIndex++]; } targetIndex++; remaining--; } }
Быстрая сортировка данных
Быстрая сортировка тоже представляет собой алгоритм, отвечающий типу «разделяй и властвуй». Сортировка данных происходит рекурсивно и поэтапно: 1. Выбирается ключевой индекс, массив делится по нему на 2 части. Выбор осуществляется разными способами, мы же возьмём случайное число. 2. Все элементы, которые больше ключевого, перемещаются в правую часть массива, которые меньше — в левую. Теперь ключевой элемент больше любого значения слева и меньше любого значения справа. 3. Первые два шага повторяются до полной сортировки массива.
Смотрим на работу алгоритма:

Выбираем ключевой элемент случайным образом:
int pivotIndex = _pivotRng.Next(left, right);

И переносим значения справа от ключевого индекса, располагая их в верном положении (используем метод

Потом повторяем этот процесс и для левой части. Рекурсивно вызываем метод
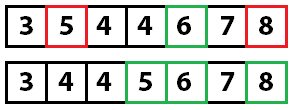
И снова быстрая сортировка:
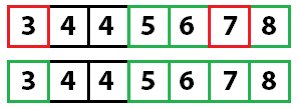
И опять:
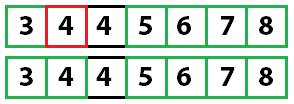
В итоге работа алгоритма завершается.
Random _pivotRng = new Random(); public void Sort(T[] items) { quicksort(items, 0, items.Length - 1); } private void quicksort(T[] items, int left, int right) { if (left < right) { int pivotIndex = _pivotRng.Next(left, right); int newPivot = partition(items, left, right, pivotIndex); quicksort(items, left, newPivot - 1); quicksort(items, newPivot + 1, right); } } private int partition(T[] items, int left, int right, int pivotIndex) { T pivotValue = items[pivotIndex]; Swap(items, pivotIndex, right); int storeIndex = left; for (int i = left; i < right; i++) { if (items[i].CompareTo(pivotValue) < 0) { Swap(items, i, storeIndex); storeIndex += 1; } } Swap(items, storeIndex, right); return storeIndex; }
Статья подготовлена специально для OTUS по материалам «Sorting Algorithms».
Хотите знать больше? Записывайтесь на курс "Алгоритмы для разработчиков"!

