Гессиан Vector-Product трюк

В некоторых алгоритмах машинного обучения возникает необходимость в расчёте матрицы вторых производных функции 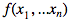Будем называть её «гессиан»: 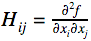Примером может быть метод Ньютона для оптимизации. Зачастую функция может зависеть от миллионов переменных. Это частый случай в глубоком обучении, где оптимизируемая функция зависит от параметров модели, и этих параметров может быть очень много. Прямой расчёт гессиана для такой функции был бы очень сложен, поскольку даже объём памяти, требуемый для хранения элементов гессиана, уже растёт как квадрат числа переменных.

Вместе с тем, далеко не всегда необходима сама матрица гессиана. Иногда нужно лишь произведение этой матрицы на какой-то вектор: Hv (например, в методе сопряжённых градиентов для оптимизации). В этом случае можно избежать вычисления всего гессиана и рассчитать всего лишь 1 производную по направлению.

Будем обозначать градиент функции 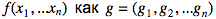и получаем:

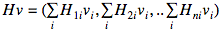Рассмотрим одну компоненту этого вектора:

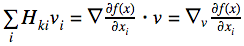Как видно, это всего лишь производная по направлению для функции 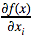И её легко сосчитать с помощью конечных разностей для произвольной функции F(x):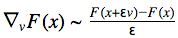Запишем итоговую формулу: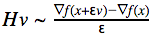

Дополнительные материалы: 1. Hessian Free Optimization; 2. Fast Exact Multiplication by the Hessian; 3. Посмотреть формулы из заметки можно здесь.

Есть вопрос? Напишите в комментариях!