Несколько слов про генеративные состязательные сети

На самом пике волне хайпа искусственного интеллекта уверенно держатся генеративные состязательные сети. Не все знают, но генеративные модели появились ещё в 18-ом веке, когда преподобный Томас Байес сформулировал своё знаменитое правило связавшее «приорное» и «постериорное» распределения. 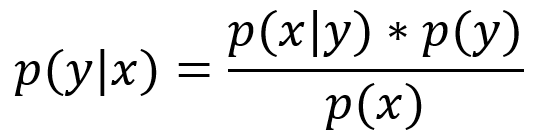Но до недавнего времени генеративный подход в решении задач машинного обучения натыкался на трудности в оценке распределения на данных ввиду его сложности. Именно эту проблему и решил (конечно, в некотором приближении) Ян Гудфеллоу в своей уже знаменитой статье «Generative Adversarial Networks», научив нас сэмплировать из этого сложного распределения.

Давайте разберёмся с ней

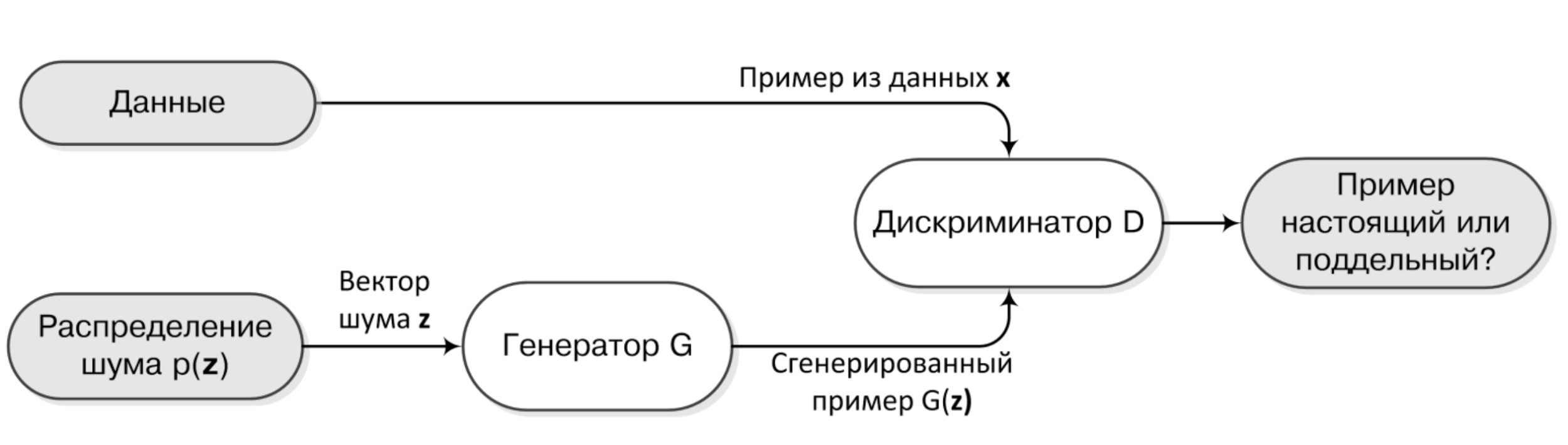Изображение из книги “Глубокое обучение”

Основная идея заключается в том, чтобы обучать одновременно две нейронные сети. Первую будем называть «Генератор» и её/его задача — породить примеры похожие на те, что есть в обучающей выборке с точки зрения второй сети — «Дискриминатора». Задача Дискриминатора же — учиться отличать порождённые генератором примеры от тех, что есть в той же обучающей выборке.

При этом Генератор, конечно, не занимается творчеством, а является, как это обычно бывает с нейронными сетями, сложной многомерной функцией, получающей на вход вектора из какого-нибудь многомерного пространства и выдающей на выходе примеры из пространства данных. 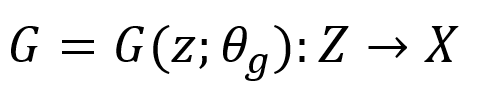Где theta — параметры сети, а Z — то самое входное пространство, на котором мы ещё и зададим приорное распределение, например N(0,1). Дискриминатор же получает на вход примеры из пространства данных и выдаёт бинарный ответ — является ли очередной пример «настоящим» или он порождён Генератором: 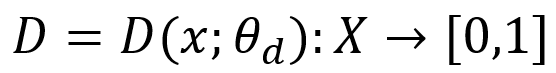Это состязание можно формализовать в виде минимаксной игры: 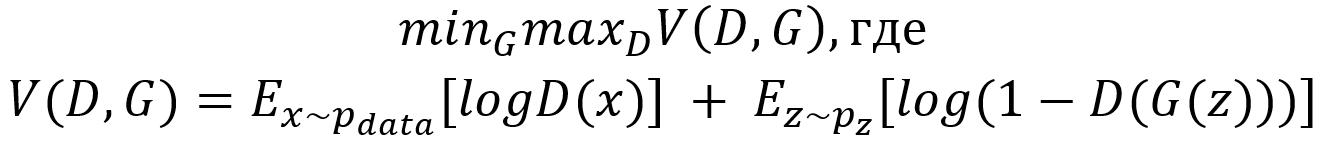И, что самое главное, существует такой набор условий, при котором мы можем математически гарантировать сходимость обучения, что в конечном счёте и обуславливает эффективность GAN'ов.

В идеальном мире в процессе совместного обучения примеры порождаемые Генератором будут всё более похожи на исходные, и, в конце концов, Дискриминатор не сможет отличить первые от вторых. На простых датасетах типа MNISTа всё так и происходит.

Картинка взята из оригинальной статьи GANs

Однако для более сложных наборов данных требуется некоторое количество дополнительного волшебства. О конкретных трюках и модификациях я расскажу в следующих постах.

Остались вопросы? Напишите в комментариях!