Математика для ИИ: математическое ожидание, дисперсия и ковариация

Математическое ожидание определяется в теории вероятностей в качестве среднего значения повторения некоторого события. Можно сказать, что ожидаемое значение функции f(x) над распределением вероятностей P(x) — это среднее значение f в случае, если x берётся из P.

Математическое ожидание определяется для дискретных случайных величин следующим образом:

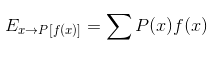
Если же речь идёт о непрерывных случайных величинах, то формула выглядит иначе:

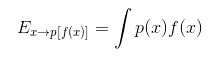
В каком-то смысле, это значение можно назвать мерой так называемого «центра» по распределению вероятностей. Но интересно узнать и то, каким образом изменятся значения функции f(x) случайной величины x, если мы возьмём различные значения из её распределения вероятностей P(x). Это не что иное, как дисперсия, представляющая собой среднеквадратичное отклонение значений f(x) от среднего значения f(x):

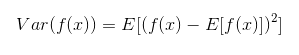
Если же говорить о корне этого выражения, то его называют стандартным отклонением. Следовательно, мы можем определить ковариацию — меру линейной зависимости 2-х случайных величин. Ковариация показывает, насколько сильно линейно связаны 2 числа:

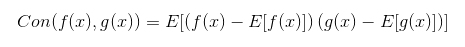
Источник: «Mathematics for Artificial Intelligence – Probability».