Динамическое программирование: не так страшен чёрт...

Часто встречаю в интернете такое: «Мне дали на 4-м туре собеседования в Яндексе задачу динамического программирования — уууу — какая сложная была!», «Сейчас крупнейшие зарубежные компании на собеседовании сразу дают динамику, чтобы отсеять слабых программистов».

Из-за устоявшихся стереотипов такие задачи считаются очень сложными. Предполагается, что решение их подвластно немногим. Что же это за страшный зверь такой — динамическое программирование?

Если разобраться, концептуально тут всё очень просто, и идея этого метода лежит на поверхности. Сперва делаем модель задачи, формализуя её и просто находим решение для параметра модели, равного, скажем, единице. Затем предполагаем, что она решена для параметра, равного N - 1, и, исходя из этого, решаем для N. Те, кто недавно учились в школе знают, что это принцип математической индукции. Не обязательно двигаться с шагом 1, достаточно уметь свести данную задачу к той же задаче, но меньшей размерности.

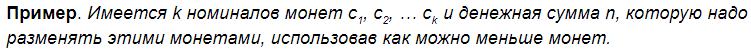
Подумав над этой задачей, вы можете решить, что стоит сначала выбрать как можно больше монет максимального номинала для того, чтобы общее количество монет было бы минимальным. Этот способ не всегда ведёт к удаче. Например, у вас есть номиналы 1, 3 и 4 коп. Нужно разменять 10 коп. Если взять максимальные доступные номиналы — 2 раза по 4 коп + 2 раза по 1 коп, это не будет оптимальным решением, поскольку есть решение лучше — 3 + 3 + 4, которое требует всего 3 монеты, а не 4.

Каков общий принцип?

Находим оптимальную комбинацию для “базы” нашей индукции. Для простоты можно взять “вырожденный” случай, когда множество номиналов — пустое и, соответственно, сумма, которую необходимо разменять, равна нулю. Очевидно, для этого нужно 0 монет.

Обозначим нашу функцию количества монет от суммы через coins. То есть, coins(0) = 0. Далее, предположим, вы нашли оптимальную комбинацию для размена суммы n. Это означает, что число монет coins(n), требуемое для размена суммы n, минимальное из возможных.

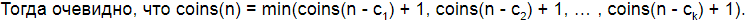Зная это рекуррентное соотношение, уже можно написать программу для его вычисления, воспользовавшись рекурсией. Для эффективности стоит закэшировать промежуточные результаты, найденные на предыдущих шагах рекурсии.

Аналогичный способ можно использовать для решения такой задачи: сколькими способами можно разменять данную сумму монетами заданных номиналов?

Как только вы видите в условии задачи “Сколько чего-нибудь длины N можно составить?” или “Каково максимальное/минимальное количество чего-нибудь при ограничении на что-то другое?”, смело можете пробовать применять этот метод: скорее всего, он приведёт к успеху.

Подробнее мы рассматриваем этот метод и решаем большое количество задач на динамическое программирование (не только решаем задачи, но и пишем программы!) на нашем курсе Алгоритмы для разработчиков. Присоединяйтесь! Ждём вас!