Оцениваем сложность алгоритмов: что такое О(log n)?

Если вы сталкивались с алгоритмами, то наверняка видели обозначения типа O(log n), а также слышали о логарифмической вычислительной сложности. Давайте освежим в памяти, что это такое, и как оценивается сложность алгоритмов.
Итак, обычно сложность алгоритмов оценивают по времени выполнения либо по используемой памяти. Как бы там ни было, сложность будет зависеть от размеров входных данных. Очевидно, что массив из ста элементов обработается быстрее, чем из тысячи. При этом здесь нас мало интересует точное время, ведь оно зависит от типа данных, процессора, языка программирования и прочих параметров. Главное — это асимптотическая сложность — сложность при стремлении размера входных данных к бесконечности.
Представьте, что какому-то алгоритму надо выполнить 4n3 + 7n условных операций для обработки n элементов входных данных. Если увеличивать n, на итоговое время работы будет намного сильнее влиять возведение n в куб, а не умножение n на 4 либо прибавление 7n. А значит, можно сказать, что временная сложность такого алгоритма равна О(n3) и она кубически зависит от размера входных данных.
Что касается заглавной О (О-нотация), то это пришло из математики, т. к. данную букву используют, чтобы сравнивать асимптотическое поведение функций. Формально O(f(n)) будет значить, что объём занимаемой памяти либо время работы алгоритма растёт в зависимости от объёма входных данных, что происходит не быстрее, чем константа, умноженная на f(n).
Линейная сложность — O(n)
Линейной сложностью обладает, к примеру, алгоритм поиска наибольшего элемента в несортированном массиве. Чтобы понять, какой элемент массива максимальный, нам понадобится пройтись по всем n-элементам этого массива.
Логарифмическая сложность — O(log n)
Тут можно вспомнить бинарный поиск. Когда массив отсортирован, можно его проверить на наличие конкретного значения по методу деления пополам. Если при проверке среднего элемента мы увидим, что он больше искомого, мы отбросим вторую половину массива. Если меньше, отбросим первую половину. И так до тех пор, пока не проверим log n элементов.
Квадратичная сложность — O(n2)
Вспоминаем алгоритм сортировки вставками. В классической реализации речь идёт о двух вложенных циклах. Первый нужен для прохождения по всему массиву, а второй — для нахождения места очередному элементу в отсортированной части. В результате, число операций зависит от размера массива как n * n, то есть n2.
Есть и другие оценки по сложности, но основаны они на том же принципе.
Также бывает, что время работы алгоритма не зависит от размера входных данных. В этом случае сложность обозначается как O(1). К примеру, чтобы определить значение третьего элемента массива не надо ни запоминать элементы массива, ни проходить по ним некоторое число раз. Здесь надо дождаться в потоке входных данных 3-й элемент, что и будет итогом, на вычисление которого для любого объёма данных потребуется одно и то же время. Схожим образом проводят оценку по памяти.
Наглядный пример
Теперь давайте посмотрим на время выполнения алгоритма определённой сложности с учётом размера входных данных и при скорости 106 операций в секунду:
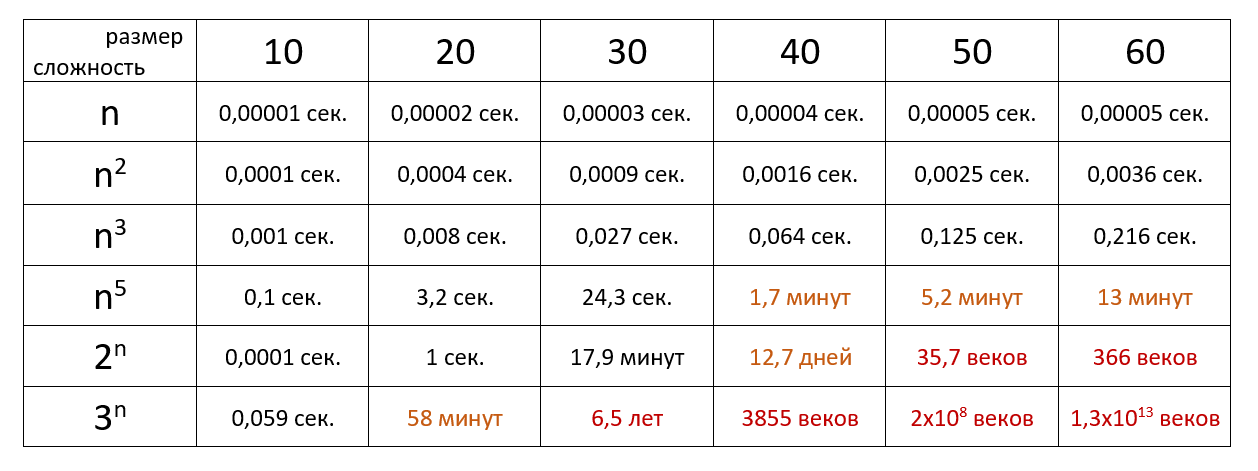
Вот и всё! Если же хотите разбираться в алгоритмах на уровне разработчика, вам сюда.

