Пост-квантовая криптография
Наверняка, многие, кто так или иначе связан с IT, слышали о том, что квантовый компьютер легко взламывает современные методы криптографии с открытым ключом. Существует множество разрозненных мнений о том, насколько скоро появится квантовый компьютер, способный «взломать» ключи той длины, которой мы пользуемся сегодня — 4096 бит RSA модуль или 256 бит подгруппа для Диффи-Хэллмана.
И всё же Агенство стандартизации NIST решило готовить сани летом и в 2018 году запустило конкурс на лучшие пост-квантовые примитивы. С предложенными кандидатами на пост-квантовую эру мы и познакомимся.
Предисловие
Современная криптография с открытым ключом (TLS, SSH, IpSec, Signal) основана на сложности факторизации больших чисел (RSA) и/или сложности вычисления дискретного логарифма (Диффи-Хэллман). В 1994 году Шор предложил квантовый алгоритм, решающий обе задачи за полиномиальное (от длины входных данных) время.
В терминологии криптоанализа такой алгоритм классифицируется как «тотальный взлом». Современные квантовые компьютеры не обладают мощностями, а именно количеством кубит, достаточными для решения этих задач в интересных для криптографии параметрах.
Сложно предсказать, когда мы получим квантовый компьютер, который сможет проводить вычисления с несколькими тысячами кубит. На всякий случай криптографы подготовили альтернативные криптографические примитивы, (предположительно) стойкие к атакам на квантовый компьютер.
Пост-квантовые решения
А именно, место теоретико-числовых задач (таких как факторизация, дискретный логарифм) могут занять:
I. Сложные задачи на евклидовых решетках
А именно, задача нахождения короткого вектора: по данному базису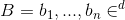 
найти кратчайший ненулевой элемент решетки, определенной как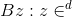 
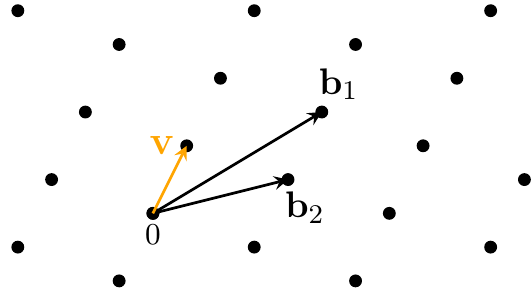
Плюсы решеток: сравнительно небольшие размеры ключей, быстрые алгоритмы генерации ключей, шифрования/дешифрования, наличие алгоритмов и для цифровой подписи, и для обмена ключами. Недостатки: плохая изученность сложности задачи короткого вектора решетки для эффективных схемах
Примеры: Frodo, New Hope, Crystals-Kyber, NTRU (для шифрования), Crypstals-Dilithium, Falcon (для цифровой подписи)
II. Сложные задачи из теории кодирования
Задача декодирования спрашивает, по данной матрице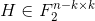 
вектору 
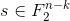и весовому значению 
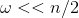найти вектор e, т.ч. He = s и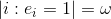 
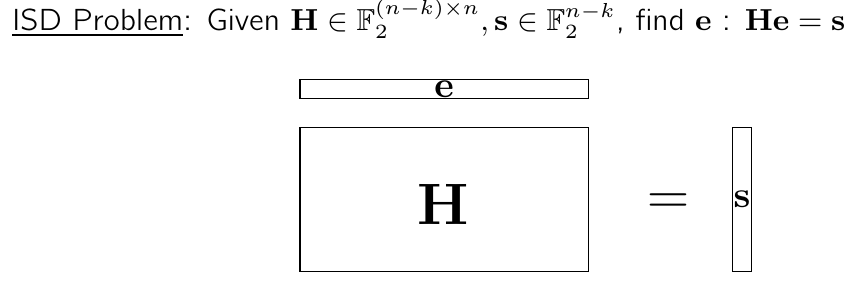
Плюсы задач теории кодирования: простота понимания, реализации; несколько десятилетий криптоанализа Недостатки: большие размеры ключа и, следовательно, более медленные операции. Отсутствие алгоритма подписи
Примеры: McEliece
III. Сложные задачи на многомерных полиномах
Найти решение (как правило, разряженное) системы уравнений от многих переменных над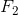 
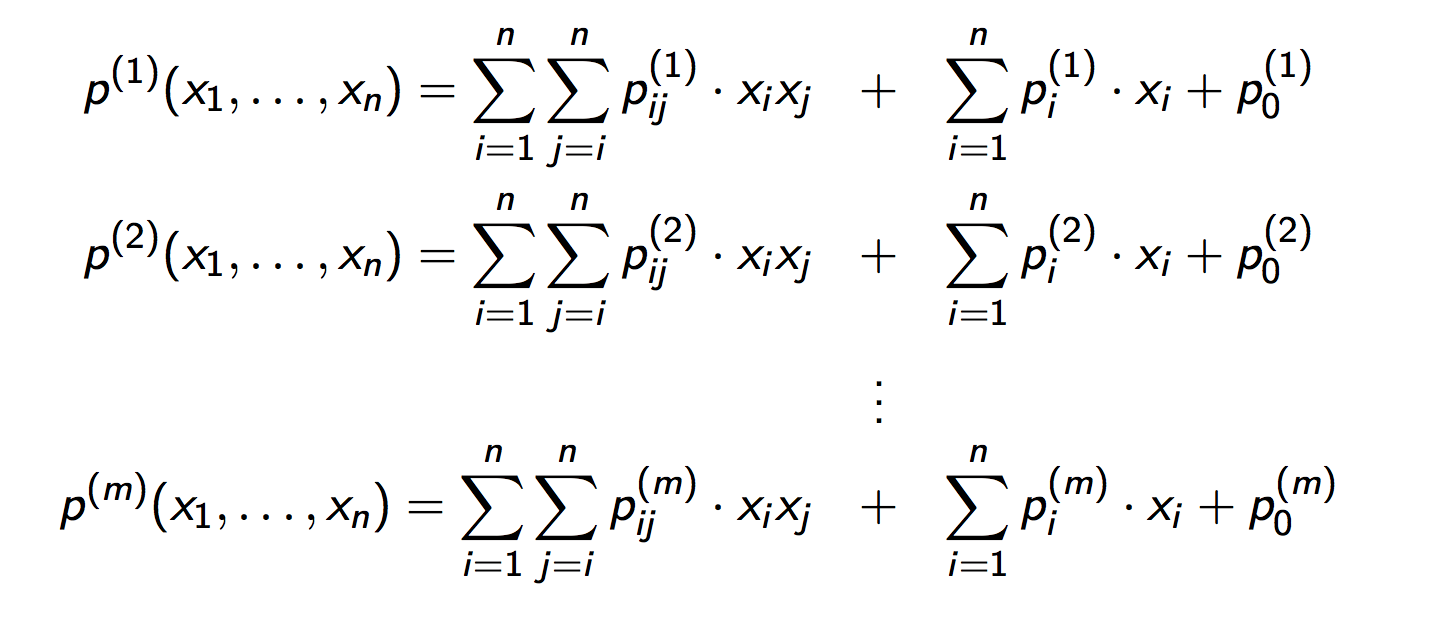Рисунок взят из презентации Albrecht Petzoldt, PQCrypto 2018
Плюсы: малый размер подписи Недостатки: сравнительно большой ключ, отсутствие алгоритма шифрования Примеры: MQDSS
IV. Задача вычисления изогении между абелевыми многообразиями
По двум (эллиптическим) кривым найти изогению определённой степени
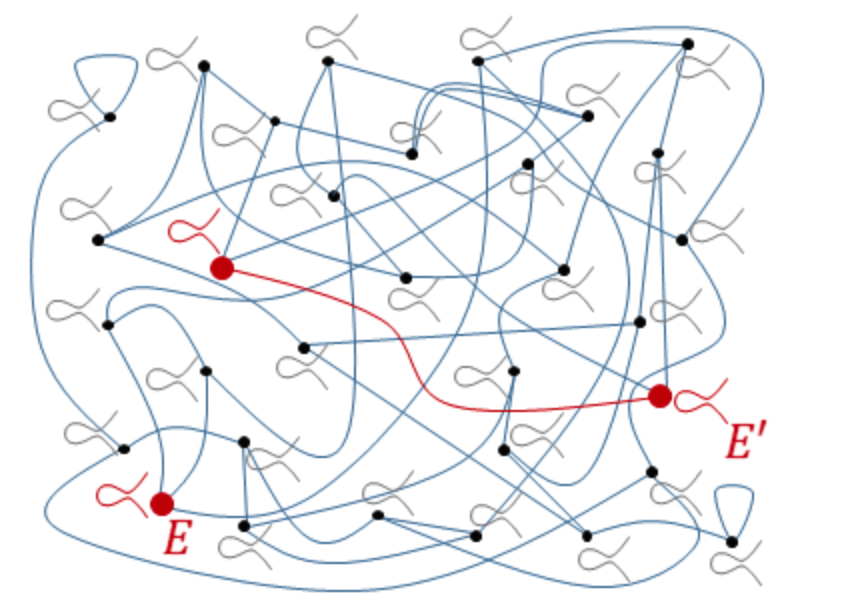Рисунок сделан W.Castryk в этом посте
Плюсы: малые размеры ключей Недостатки: сравнительно мало изученная задача, длительные алгоритмы обмена ключами, подписи еще более неэффективные Примеры: SIKE, CSIDH
V. Задача нахождения коллизий хэш-функции
По сути, усложнение одноразовой подписи Лампорта
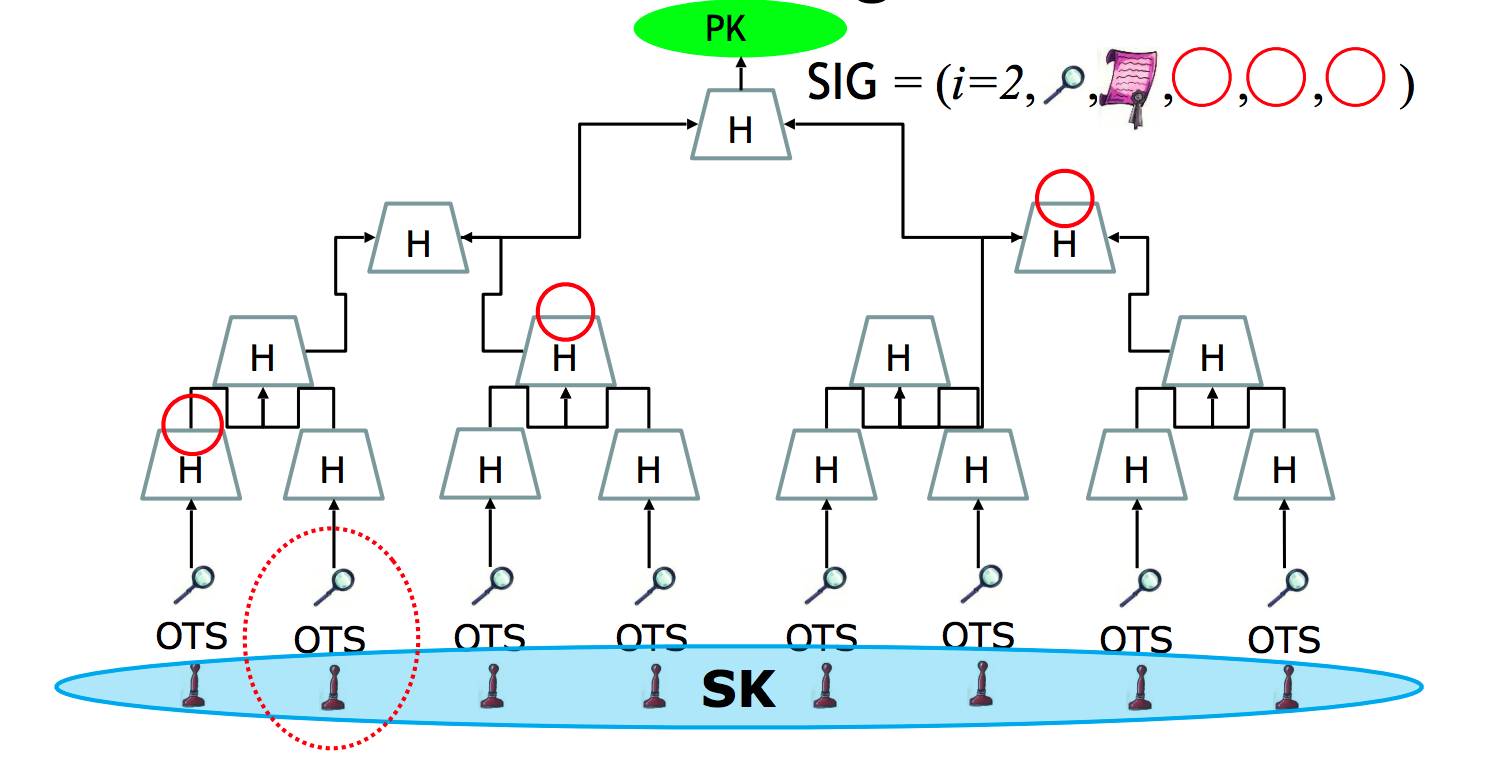
Рисунок взят из презентации Andreas Huelsing
Плюсы: небольшие ключи Недостатки: только подпись, сравнительно большой размер подписи
Примеры: SHINCS
Есть вопросы? Пишите в комментариях!
