Матричная факторизация
В последнее время всё чаще возникает потребность том, чтобы объяснить, как тот или иной алгоритм машинного обучения принимает решения. Статья обещает дать интерпретацию эмбеддингам матричной факторизации. Материал представляет собой обзор научной работы "Matrix Factorization for Collaborative Filtering Is Just Solving an Adjoint Latent Dirichlet Allocation Model After All".
Краткое содержание
В алгоритмах матричной факторизации (МФ) для каждого пользователя и каждого айтема необходимо дать числовую оценку, по которой потом проводится ранжирование айтемов в соответствии с предпочтениями пользователей. Причём используется вариант:
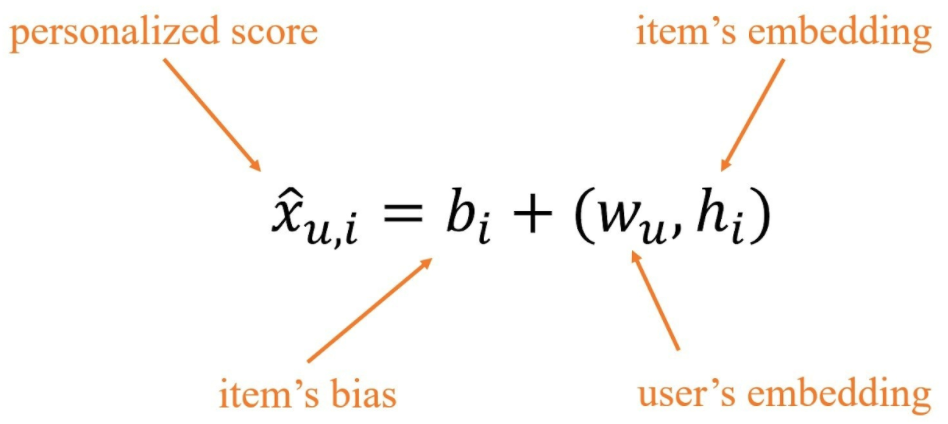
В статье авторы приводят собственную модификацию латентного размещения Дирихле для рекомендательных систем. Затем они показывают, что по эмбеддингам МФ можно получить неотрицательные эмебеддинги пользователей и айтемов, которые вводят такое же упорядочивание, что и исходные. После этого приводится доказательство, что полученные неотрицательные эмбеддинги могут выступать параметром категориального распределения в порождающем процессе модели авторов.
Предполагается, что существует несколько латентных когорт пользователей, причём внутри каждой когорты частоты встречаемости айтемов фиксированные (подбираются в процессе обучения модели). Для каждого пользователя из распределения Дирихле сэмплируется параметр тета, который отвечает за принадлежность пользователя к когортам, а далее выполняется следующий порождающий процесс построения пула рекомендаций:
1) сэмплируется когорта из категориального распределения с параметром тета;
2) сэмплируется айтем из категориального распределения, учитывающего частоты встречаемости взаимодействий с айтемами в когорте, популярность айтема и желание пользователя получать рекомендации.
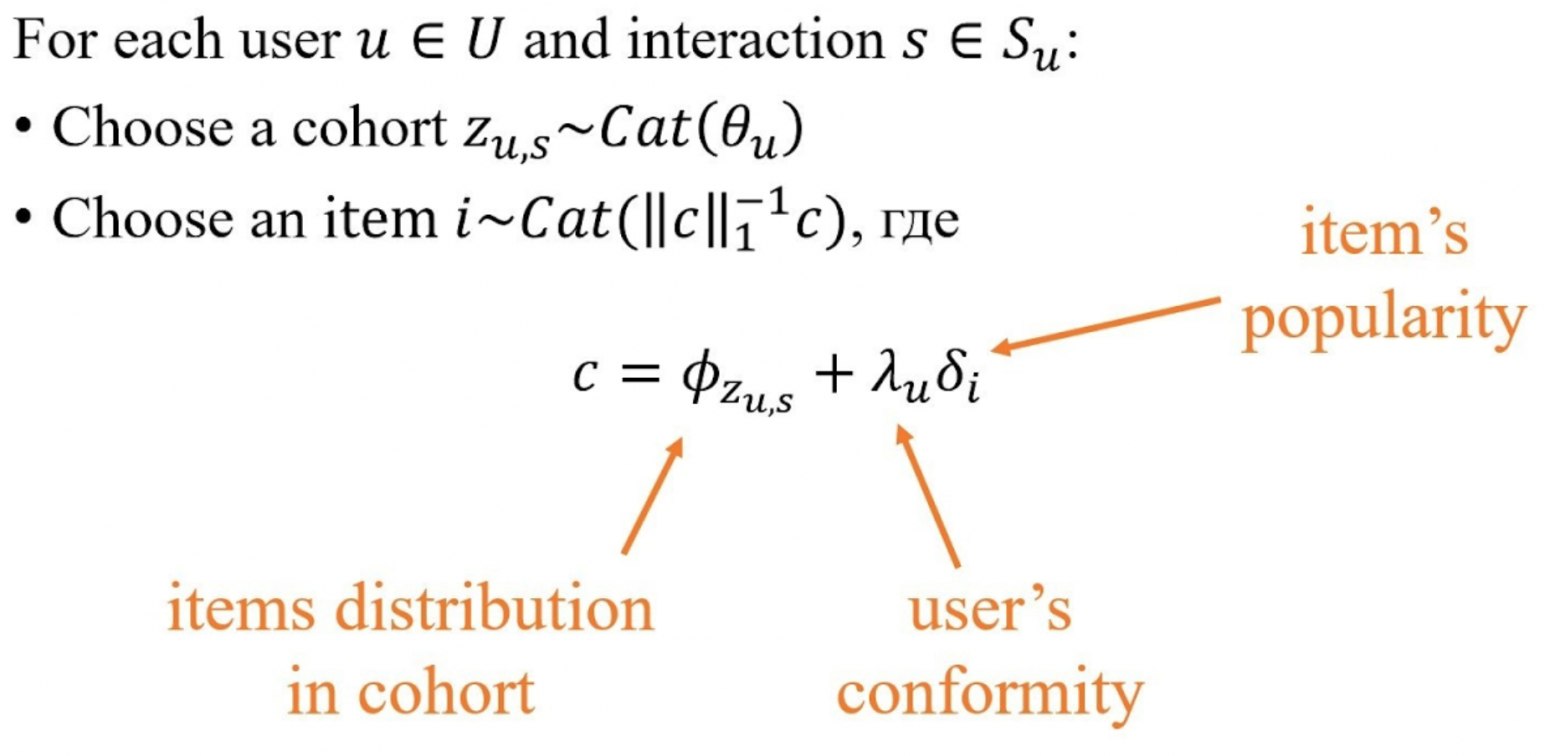
По мнению автора параметры фи, лямбда и дельта имеют логнормальные распределения, параметры которых также подбираются в процессе обучения.
Какие остаются вопросы
Нельзя быть уверенным, что объяснение тематического моделирования на языке смеси распределений будет более понятно для пользователей, чем объяснение на языке эмбеддингов.
Нет сравнения описанной модели с какими-либо методами, кроме методов матричной факторизации.
Больше материалов смотрите в моем блоге на Хабре: https://habr.com/ru/users/netcitizen/.