Введение в структуры данных. Какие структуры данных следует знать программисту?
Структуры данных — важная часть разработки программного обеспечения. А еще это распространенная тема вопросов на собеседованиях. Прочитав краткое введение в структуры данных, вы получите преимущество при приеме на работу. В своей совокупности эти знания могут пригодиться и при написании высокопроизводительного кода. Дополнительно в статье будут рассмотрены временные сложности соответствующих алгоритмов (algorithms).
Связные списки
Одна из основных структур данных. Связный список нередко сравнивают с массивом, ведь множество других структур можно реализовать или посредством массивов, или посредством связного списка.
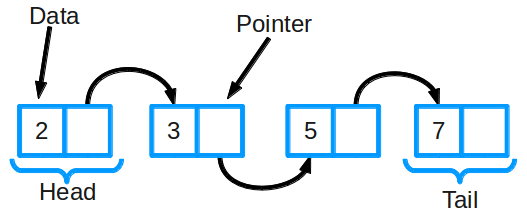
Связный список включает в себя группу (совокупность) узлов, вместе представляющих собой последовательность. Каждый из этих узлов включает в себя: — фактические данные, которые хранятся, причем и их можно представить любым типом данных; — указатель (ссылку) на последующий узел в последовательности.
Также бывают дважды связанные списки — в них каждый узел содержит указатель как на следующий, так и на предыдущий элемент списка.
Основные операции в связанном списке: — добавление в список элемента; — удаление элемента; — поиск в списке.
Временная сложность:
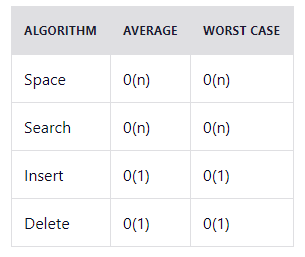
Стеки
Базовая структура данных, используя которую, можно лишь вставлять/удалять элементы, находящиеся в начале стека. Если дать определение стека простыми словами, то его можно сравнить со стопкой книг. Когда вам хочется посмотреть на книгу из середины стека, вам прежде придётся взять тома, лежащие сверху.
Тут уместно вспомнить принцип LIFO (Last In First Out) — последний добавленный в стек элемент является первым элементом, который выходит из стека.
Главные операции стеков: — вставка элемента («push»); — удаление («pop»); — отображение содержимого стека («pip»).
Временная сложность:
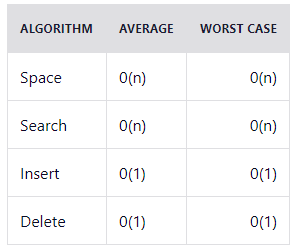
Очереди
Эту структуру данных часто сравнивают с очередью в продуктовом супермаркете. Тот, кто стоит первым, обслуживается раньше других.
С точки зрения доступа к данным, очередь — это FIFO (First In First Out). После добавления нового элемента те компоненты, которые добавили ранее, удаляются до того, как удалится новый элемент.
Операции: — enqueue — вставка элемента в конец очереди; — dequeue — удаление переднего компонента.
Временная сложность:
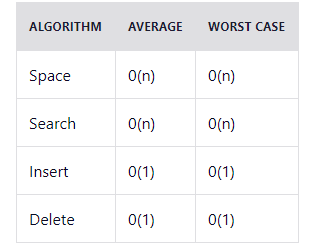
Реализацию на практике можно посмотреть здесь
Множества
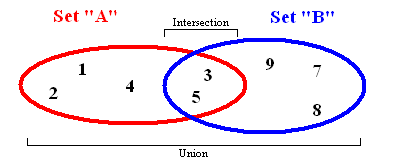
Во множествах данные хранятся без конкретного порядка, причем повторяющиеся значения отсутствуют. Кроме стандартных возможностей по добавлению и удалению, существуют другие важные функции, поддерживающие одновременную работу с 2-мя наборами: • Union (объединение). Все элементы из 2-х разных множеств объединяются, причем результат возвращается как новый набор; • Intersection (пересечение). При наличии двух заданных множеств функция вернет иное множество, которое будет включать в себя элементы, находящиеся и в первом множестве, и во втором; • Difference (разница). Возвратится перечень элементов, находящихся в одном множестве, но не повторяющихся в другом; • Subset (подмножество). Вернется булево значение, которое покажет, содержит ли одно множество все компоненты другого множества.
Map’ы
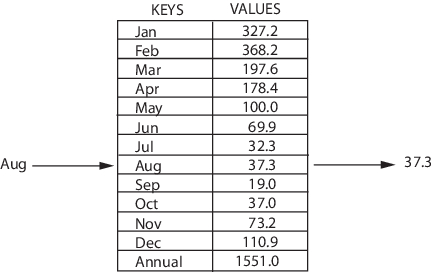
Map представляет собой структуру данных, хранящую эти данные в парах ключ-значение, причем каждый ключ является уникальным. Также эту структуру называют словарем или ассоциативным массивом и часто используют для поиска данных. В совокупности map’ы позволяют: — добавлять в коллекцию пары; — удалять из коллекции пары; — менять существующие пары; — искать значения, связанные ключом.
Хэш-таблицы
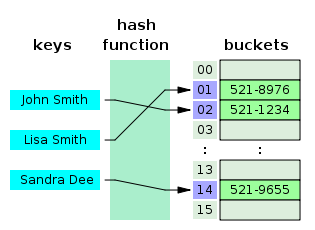Хэш-таблицами называют структуры данных, реализующих map-интерфейс. Такая таблица задействует хэш-функцию в целях расчета индекса в массиве, по которому можно определить искомое значение. В среднем обеспечивается эффективное время поиска O (1).
Хэш-функция принимает строку, возвращая число, то есть для одного и того же ввода она должна возвращать одно и то же число. Если же 2 ввода хэшируются одинаковым цифровым выходом, речь идет о коллизии — коллизий должно быть как можно меньше.
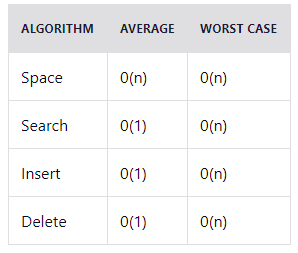
Временная сложность алгоритма:
JS-код хэш-таблицы для практики
Бинарное дерево поиска
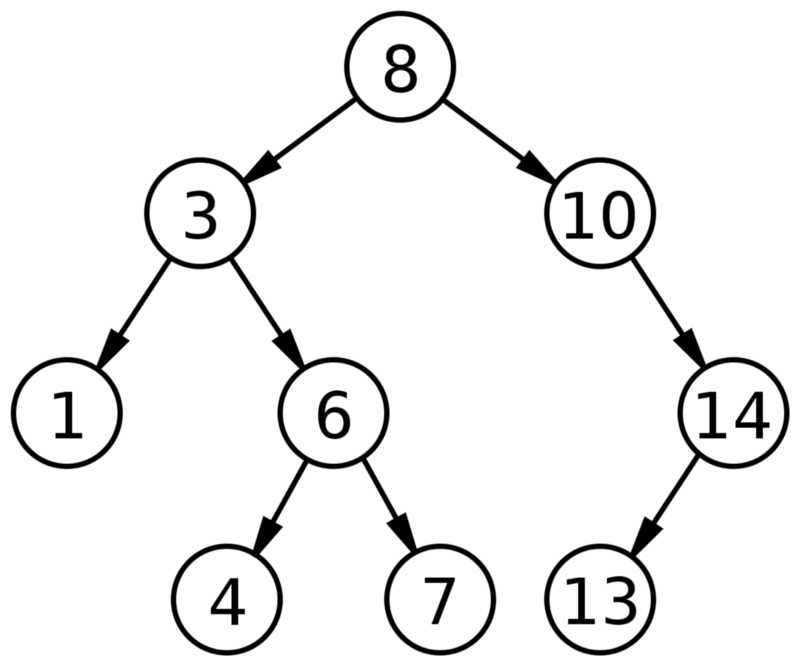
Деревом называют структуру данных из узлов. Такие данные характеризуются следующим образом: 1. У каждого дерева есть корневой узел (вершина). 2. Корневой узел содержит ноль либо более дочерних узлов. 3. Любой дочерний узел аналогично содержит ноль и более дочерних узлов и т. п.
Также из теории: 1. Каждая вершина содержит до 2 потомков. 2. Для любой вершины левые потомки меньше текущего узла.
Двоичные (бинарные) деревья поиска обеспечивают быстрое нахождение, добавление и удаление компонентов. При задании настроек следует учитывать, что в среднем любое сравнение дает возможность операциям пропускать половину дерева, поэтому поиск, вставка либо удаление отнимает время, значение которого пропорционально логарифму числа хранящихся в древе компонентов.
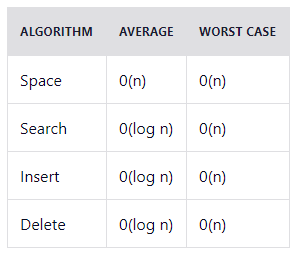
Временная сложность алгоритма:
Префиксное дерево
Эта структура тоже представляет своеобразное дерево поиска. Данные хранятся в шагах, а каждый из шагов — это узел дерева. Благодаря быстрому поиску и наличию функции автозаполнения структура чаще применяется для хранения слов.
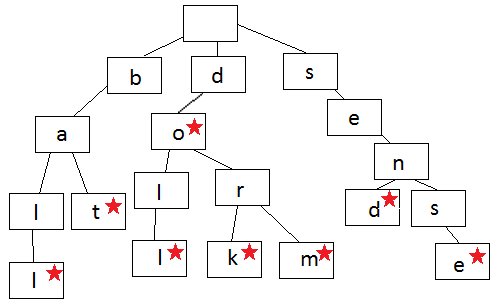
Согласно теории, каждый узел включает в себя одну букву слова. Чтобы записать слово, пользователь следует ветвям дерева, что позволяет записать слово побуквенно. Когда слово заканчивается либо порядок букв становится отличен от других слов, шаги расходятся. Каждый узел включает букву и логическое значение, которое указывает, является ли этот узел последним в слове.
Глядя на картинку выше, можно решать задачи по самостоятельному созданию слов. Дерево, размещенное на рисунке, содержит: — ball, — bat, — dork, — dorm, — doll, — do, — send, — sense.
Бинарная куча
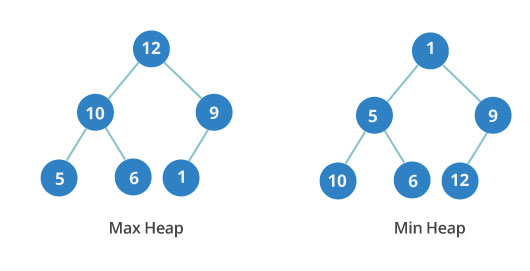
Очередное дерево, в любом узле которого содержится не больше 2-х детей. Эта структура — полное дерево, то есть все уровни заполнены вплоть до последнего уровня, причем последний уровень наполняется слева направо.
Согласно теории, бинарная куча бывает: — минимальной — ключи родительских узлов ≤ ключам дочерних компонентов; — максимальной — ключи родительских узлов ≥ значениям детей.
Приоритетное значение имеет порядок между уровнями, а не вершинами. На картинке 3-й уровень минимальной кучи включает в себя числа 10, 6 и 12, которые расположены не по порядку.
Временная сложность:
Графы
Графы — совокупности вершин и связей между ними (связи называют ребрами). Также графы иногда называют сетями.
Простейший и самый понятный пример графа — соцсеть. Вершины — это пользователи, ребра — дружба между пользователями.
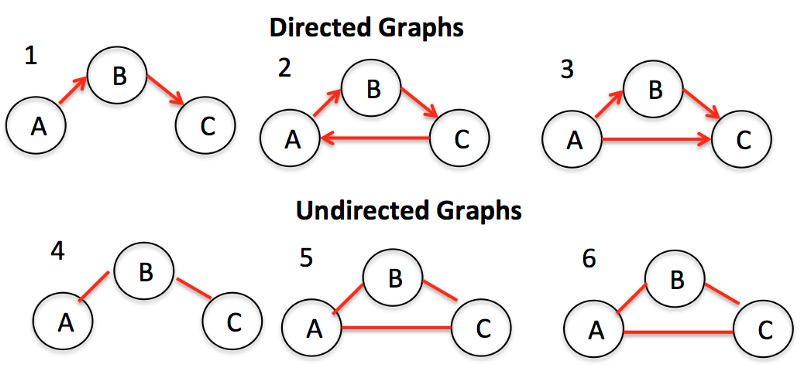
Виды графов: — ориентированные — графы с направлением на ребрах между вершинами; — неориентированные — графы без направления на ребрах.
Наиболее частые способы представления таких структур — матрица смежности и список смежности.
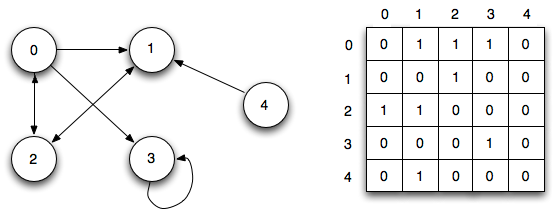
Более подробную информацию об этой структуре смотрите здесь.
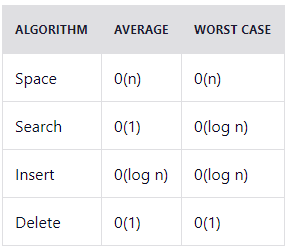
Временная сложность:
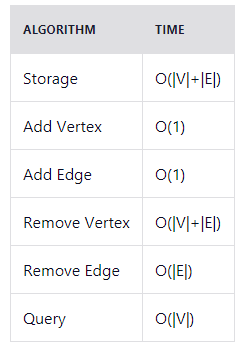
Очень надеемся, что это краткое теоретическое введение в структуры данных и методы их хранения будет полезно читателям. Если же интересуют более продвинутые знания, обратите внимание на курс «Алгоритмы для разработчиков». Это содержательный курс, включающий в себя много практических заданий и полезной информации об алгоритмических структурах, которые могут понадобиться современному разработчику. Пройдя курс, вы сможете решать задания по алгоритмам, улучшите качество кода и его структуру, повысите производительность программ.
