Графы. Алгоритм Дейкстры

Статья расскажет о базовых понятиях теории графов, а также о некоторых известных алгоритмах графов. Отдельное внимание будет уделено алгоритмической последовательности Дейкстры (Dijkstra's algorithm).

Из теории

Граф представляет собой абстрактный объект из множества вершин (узлов) и набора ребер – связей между парами вершин. Эта тема чрезвычайно обширна — в той же Википедии соответствующей терминологии уделена целая страница. Более точное определение можно получить в дискретной математике, где изучают графы (их появлению способствовали работы Эйлера).

На практике графы используются при описании сложно структурированных данных, поэтому можно говорить об их большом прикладном значении. Их можно встретить в следующих случаях: — в моделях глобальной либо локальной сети; — в генеалогических древах; — в алгоритмических блок-схемах; — в схемах метро; — в принципиальных электрических схемах; — в ментальных картах; — в моделях связи в БД и во многих других случаях.

Для примера рассмотрим неориентированный граф G. Он представляет собой упорядоченную пару G:=(V, E), где:

• E — множество пар вершин (ребер);
• V — непустое множество вершин (узлов).

Ребра и узлы графа — это его элементы, количество узлов называют порядком, а количество ребер — размером.

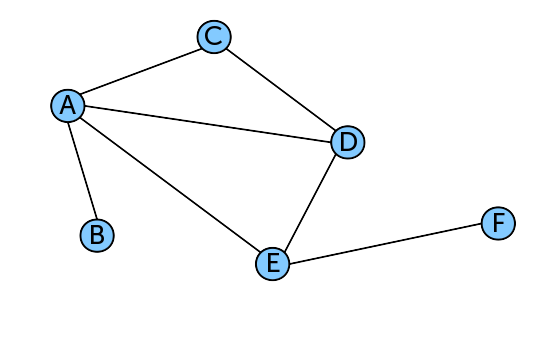
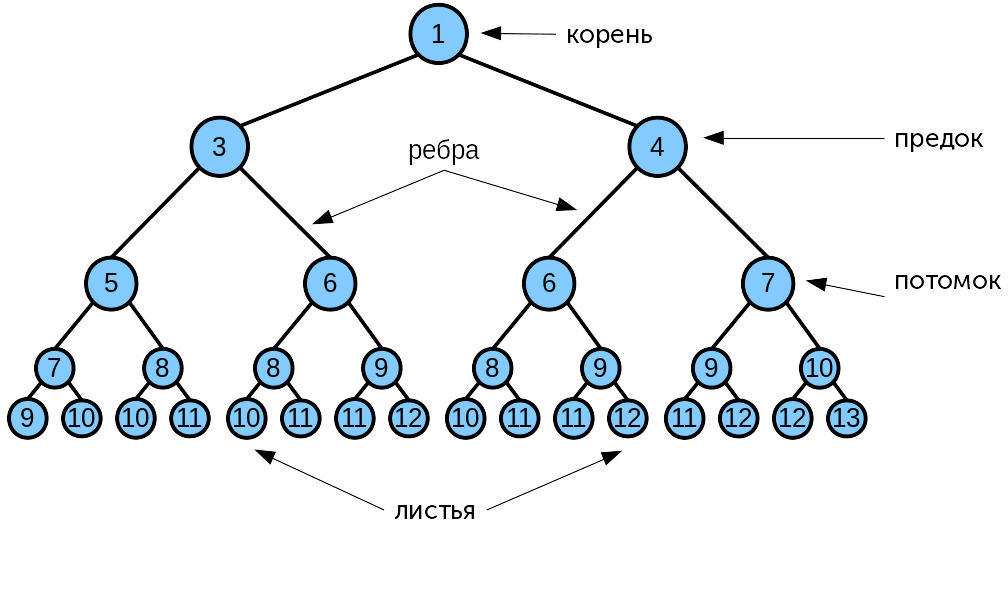
На рисунке ниже представлен связный ацикличный граф — дерево:

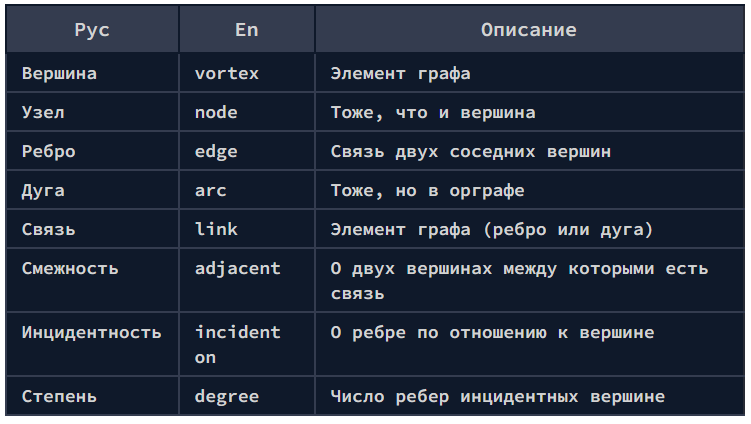
Словарь терминов

В таблице ниже представлена выборка основных терминов из теории алгоритмов графов:

Следует рассмотреть главные понятия: 1. Маршрут — конечная последовательность узлов, где каждый узел за исключением последнего соединяется со следующим с помощью ребра. 2. Цепь — маршрут, не имеющий повторяющихся рёбер. Простая цепь — маршрут без повторяющихся узлов. 3. Ориентированный маршрут (путь) в орграфе — конечная последовательность дуг и узлов, где каждый элемент инцидентен как предыдущему, так и последующему. 4. Длина пути (цикла) — количество ребер, составляющих этот путь. 5. Цикл (путь)— цепь, где совпадают первый и последний узел. Путь простой, если ребра не повторяются, а также элементарный, если является простым, и не повторяются узлы. 6. Матрица смежности, матрица инцидентности, список смежности, список ребер — методы представления графов.

Виды графов:

1. Ориентированный – (орграф) — рёбрам присвоено направление.
2. Неориентированный – пара узлов упорядоченной не является.
3. Связный — между любой парой узлов есть хотя бы один путь.
4. Дерево — связный ациклический граф (нет циклов, между парами вершин есть лишь по одному пути). Здесь корень дерева — это узел, имеющий нулевую степень захода, а листья — узел с нулевой степень исхода.
5. Взвешенный – каждому ребру поставлено в соответствие определенное число — вес ребра.

Ищем кратчайший путь в графе. Алгоритм Дейкстры

Хорошо известен алгоритм графов, который был изобретён в 1959 году учёным Эдсгером Дейкстрой (Нидерланды). Он позволяет находить кратчайшие пути от одной из вершин до всех остальных. Сегодня алгоритм графов, который создал известный ученый Дейкстра, часто применяется в программировании и других технологиях — в тех же протоколах маршрутизации. В этом алгоритме графов дан взвешенный орграф G(V, E), не имеющий дуг отрицательного веса. Надо найти кратчайшие пути от какой-либо вершины a графа G до остальных узлов.

Идея алгоритма графов следующая: надо определить массив D[], где для любой вершины v будет храниться текущая длина D[v] кратчайшего пути из s в v. Изначально D[s]=0, причем для всех остальных узлов данная длина равна бесконечности (речь идет о некотором значении, которое заведомо больше возможной длины пути).

Также для каждой вершины мы сохраняем v, несмотря на то, помечена она либо ещё нет, то есть определяется булевский массив U[]. Поначалу все узлы не помечены, поэтому первоначальное значение элементов массива — false. Сам дейкстровский алгоритм состоит из n итераций (по числу узлов), а на очередной итерации выбирают вершину v с самой маленькой величиной D[v] среди тех, которые ещё не помечены.

Выбранная вершина v отмечается помеченной, после чего на текущей итерации из узла v выполняются релаксации — просматриваются все ребра (v, to), которые исходят из вершины v, причем для каждого узла to алгоритм пробует улучшить значение D[to].

Если длина текущего ребра = len, то в коде релаксация будет выглядеть следующим образом:

В конечном итоге после n итераций, все узлы станут помеченными, а алгоритм закончит работу.

Если же не все вершины являются достижимыми из вершины s, тогда значения D[v] так и останутся для них бесконечными. В результате несколько последних итераций алгоритма станут как раз выбирать эти вершины, однако выполнять полезной работы эти итерации не станут (бесконечное расстояние не способно прорелаксировать другие). То есть алгоритм можно сразу останавливать, делая это в тот момент, когда в качестве выбранной вершины будет браться вершина, имеющая бесконечное расстояние.

На рисунке ниже — взвешенный граф, иллюстрирующий работу этого алгоритма графов в программе на C++:

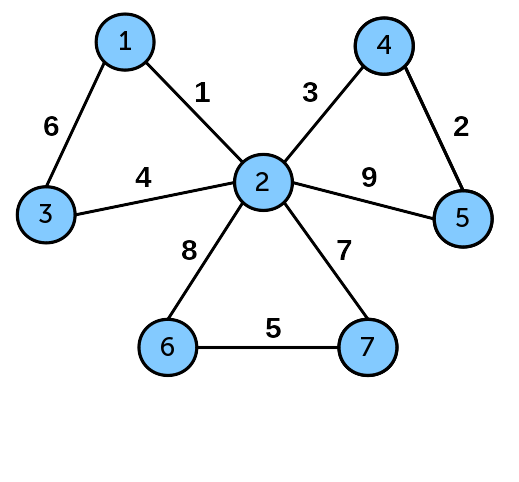
А вот и сам код программы:

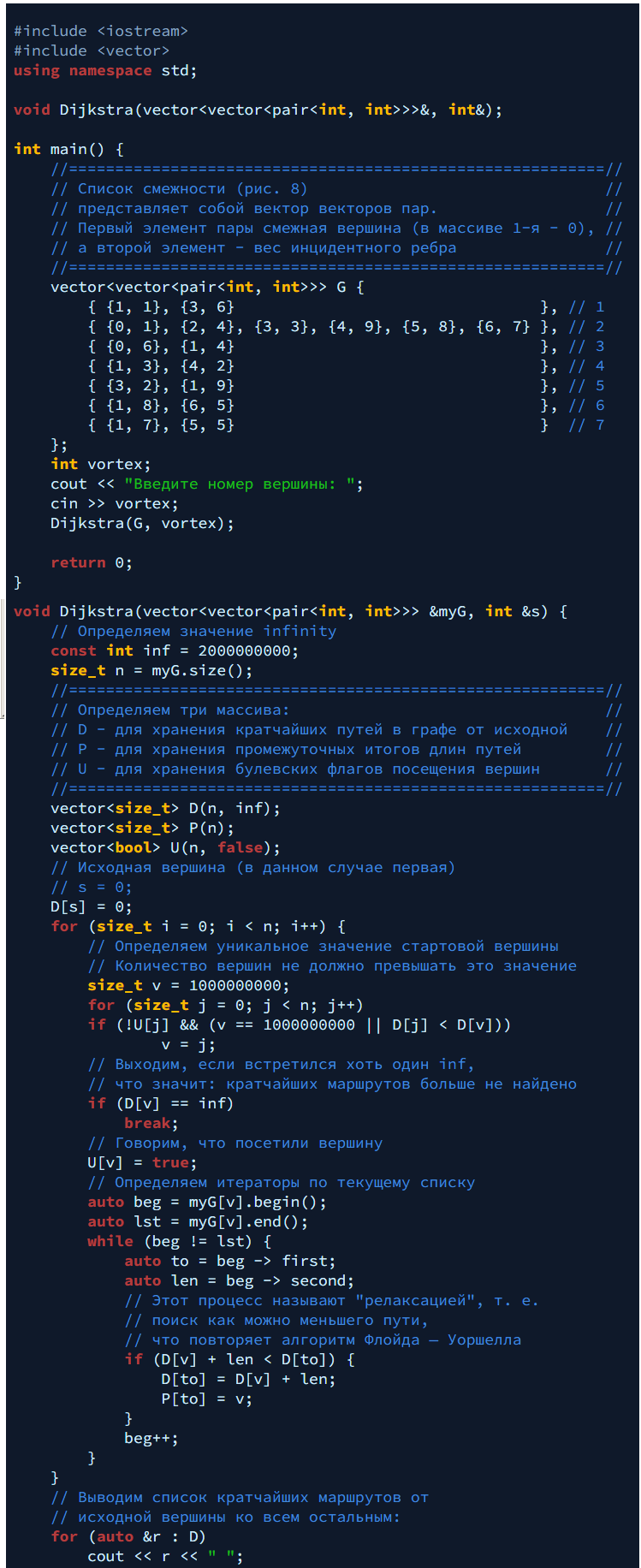
Вместо заключения

Ниже будут представлены еще два популярных алгоритма обхода графа — поиск в глубину и поиск в ширину.

Поиск в глубину

Из названия понятно, что в процессе обхода графа мы идем «вглубь», насколько это возможно. Так удастся последовательно обойти все вершины, доступные из начальной. Когда ребро приведет в непройденную вершину, алгоритм запустится с нее. Если ребер, ведущих в нерассмотренную вершину, больше не будет, произойдет возврат назад.

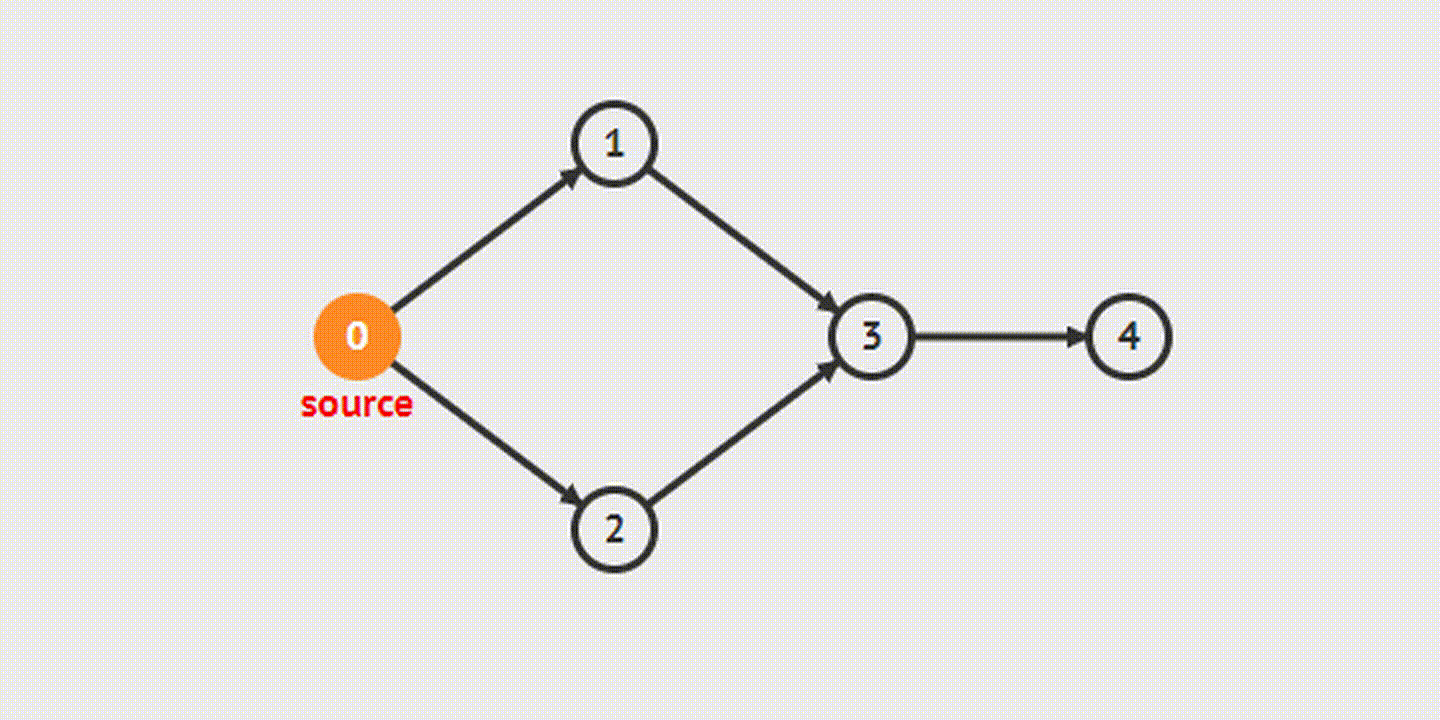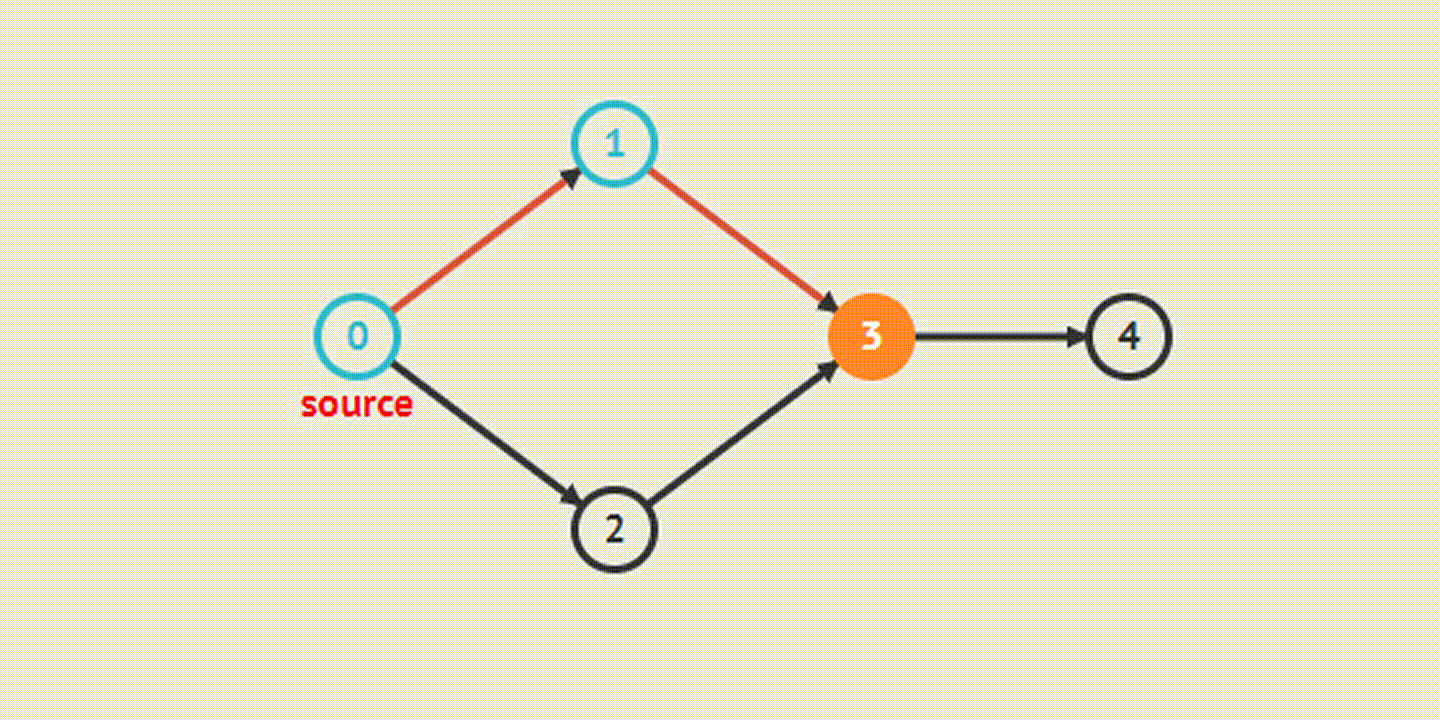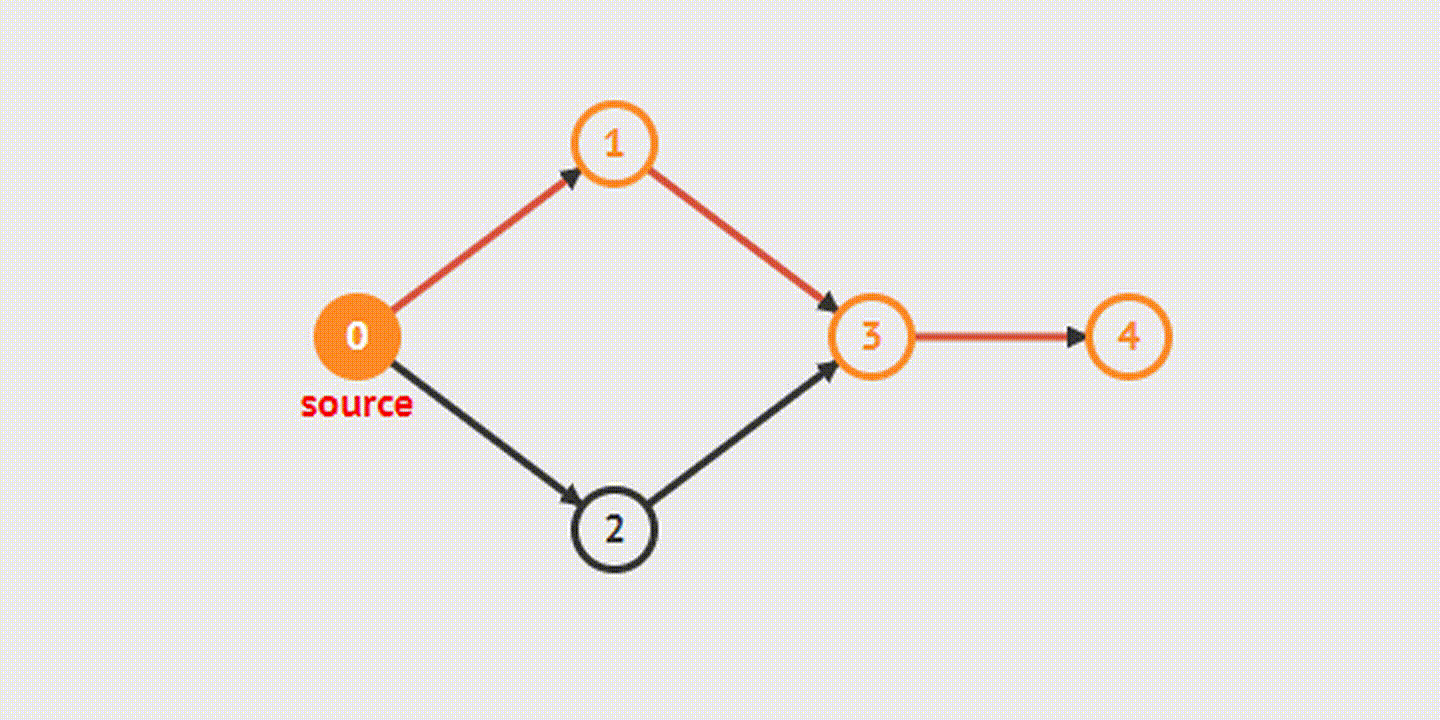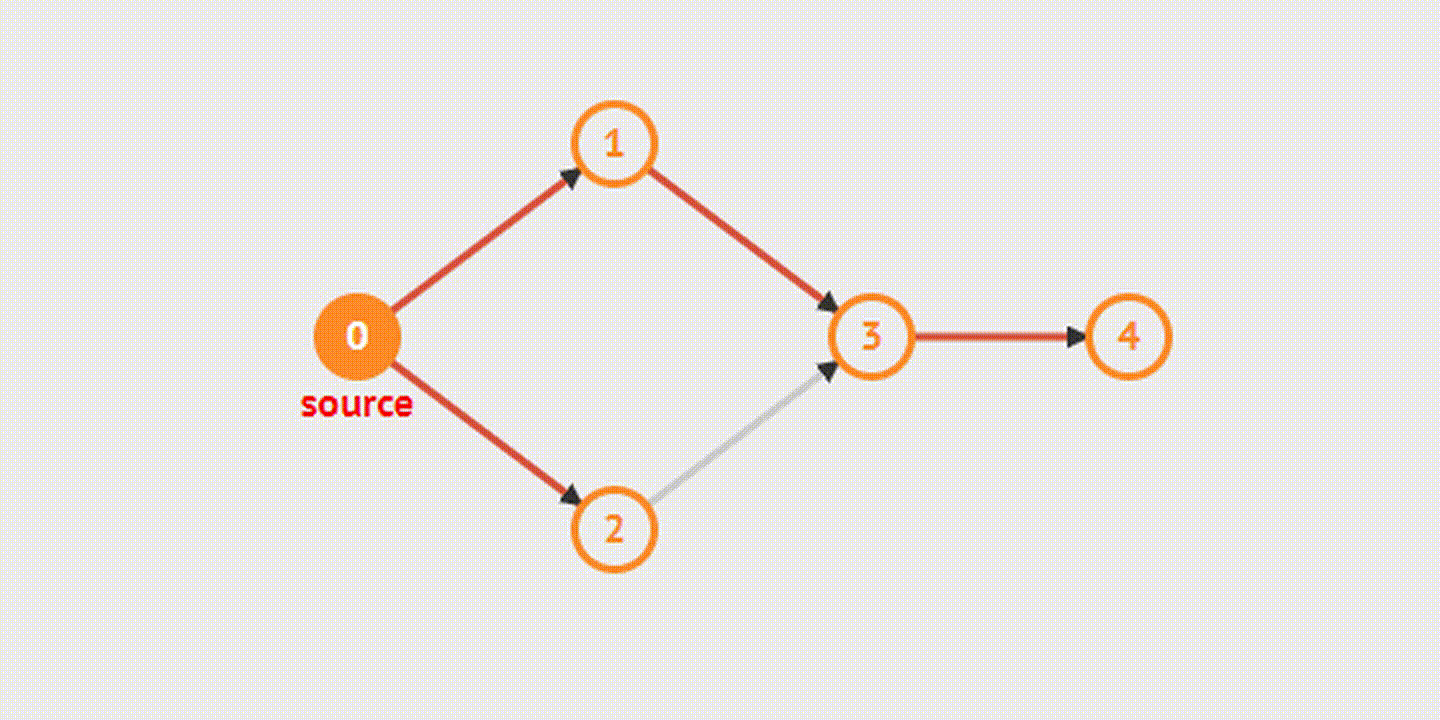
Поиск в ширину

Этот алгоритм позволит найти кратчайший путь из одной вершины до остальных. Сначала посещаются все вершины, которые смежны с текущей, далее — их потомки.

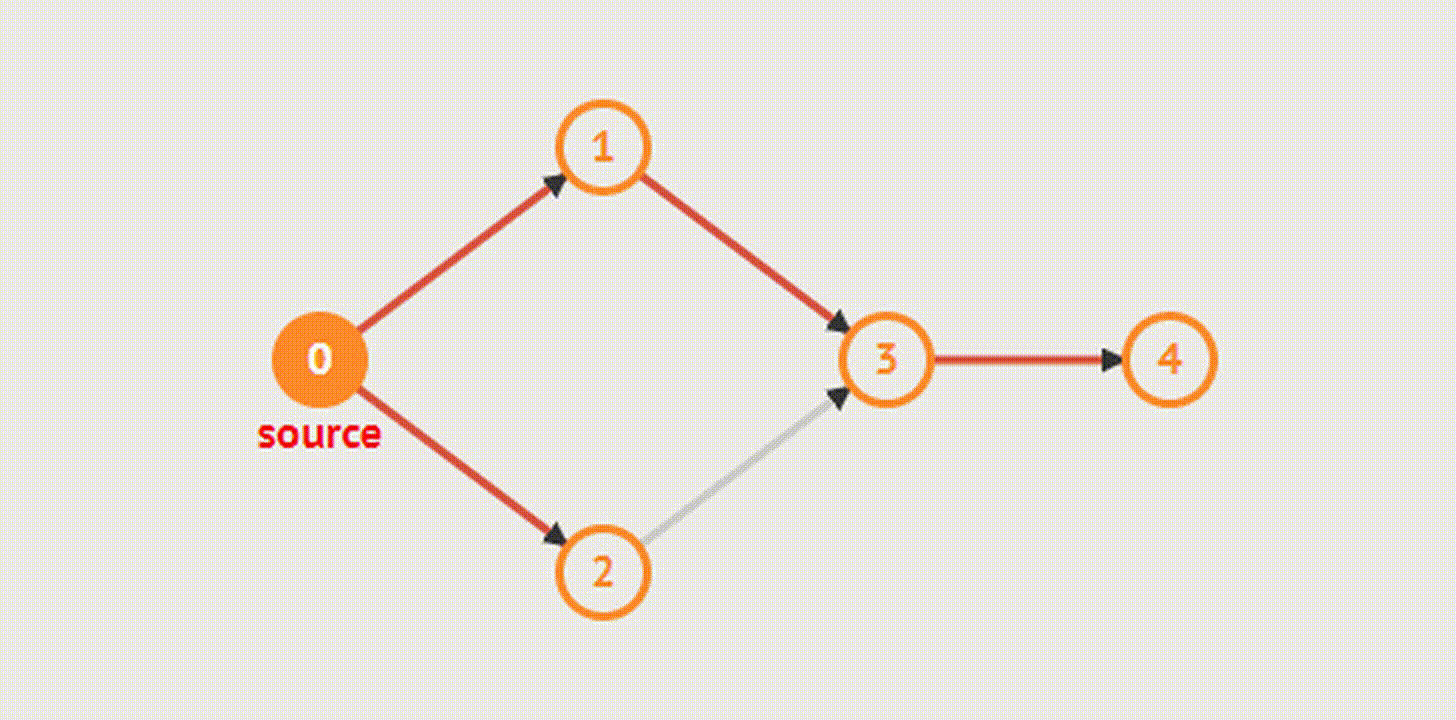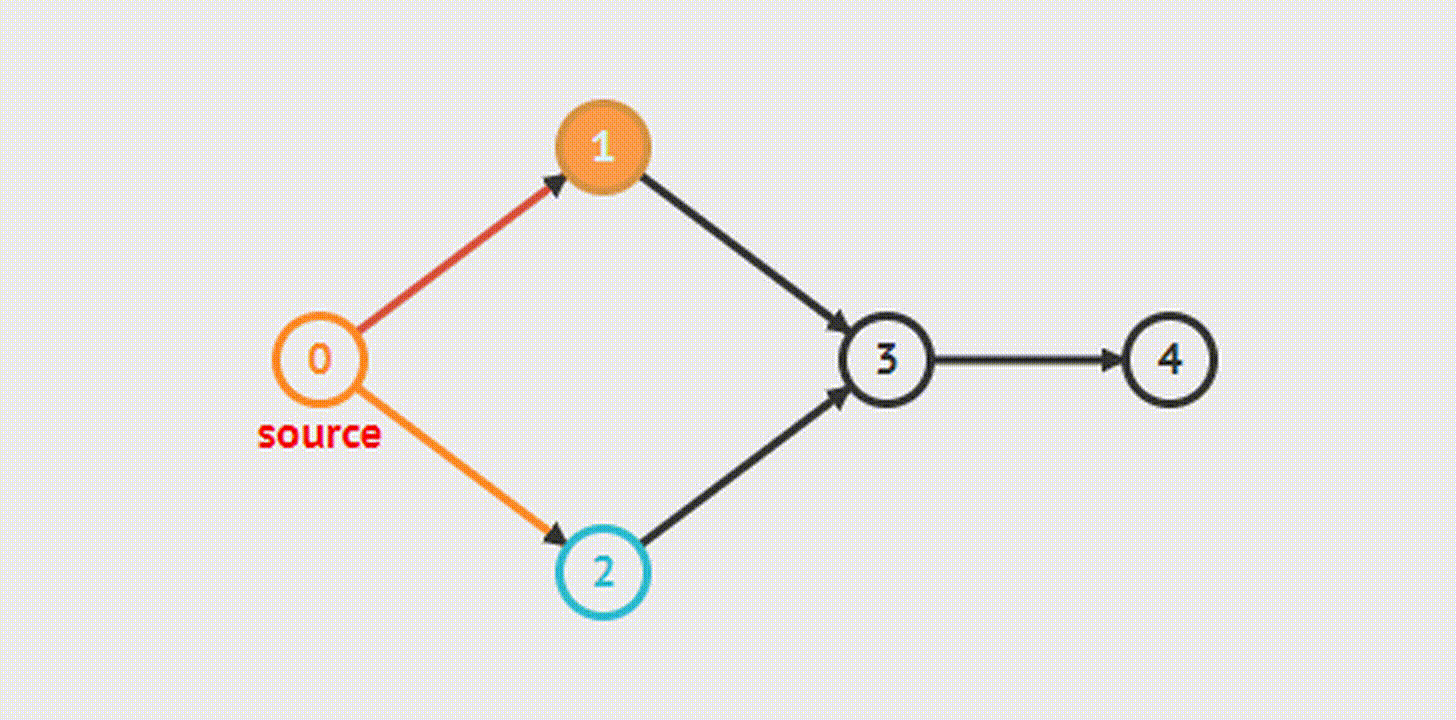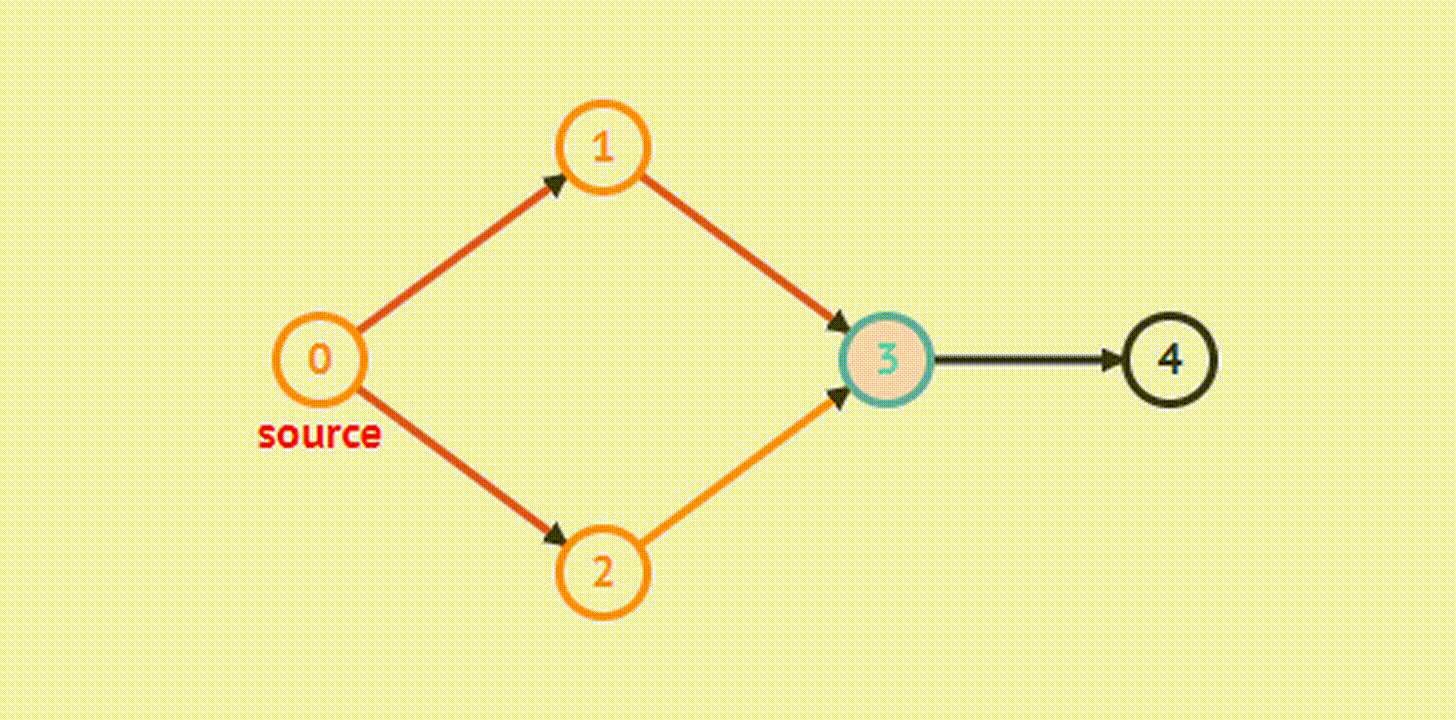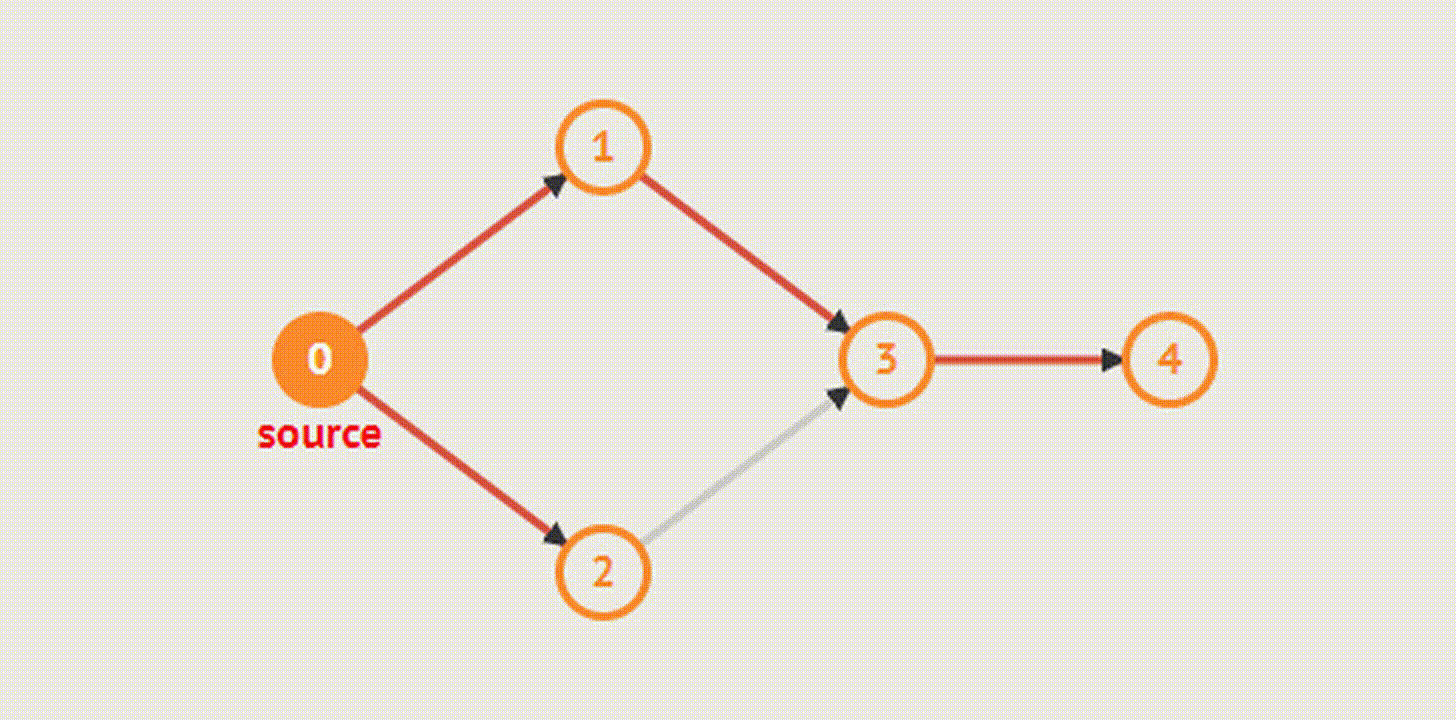
Также существуют алгоритмы Форда, Косарайю, Тарьяна и другие.

Источники: • http://inf-w.ru/?page_id=7359; • https://proglib.io/p/graphs-algoguide/.