Математика для ИИ: базовые термины теории вероятностей
Когда речь идёт об ИИ, хаотичность и неопределённость проявляются во многих формах. И теория вероятностей предоставляет нам методы для работы с неопределённостью, а также используется для анализа частоты возникновения событий.
Вероятность — это возможность осуществления чего-либо. Можно сказать, что это число от 0 до 1, причём 0 указывает на невозможность возникновения события, а единица указывает на достоверность возникновения этого события. Таким образом, вероятность возникновения события A можно обозначить P(A) либо p(A). И если P(A) = 1, событие A произойдёт точно, а если P(A) = 0, событие точно не произойдёт. В итоге мы можем вывести дополнение события P(Ac). Оно будет иметь значение P(Ac) = 1 – P(A) и обозначать вероятность того, что событие A не произойдёт никогда.
Теперь поговорим о вероятностях нескольких событий и взаимодействиях между этими событиями. Для этого нам пригодится термин совместная вероятность, представляющая собой вероятность того, что оба события произойдут. Если события независимы, то совместную вероятность мы можем определить следующим образом:
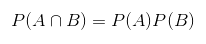
Но если события взаимоисключают друг друга, наша формула усложнится:
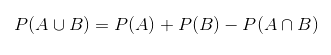
Теперь приведём ряд терминов, используемых во время вычисления вероятности. Какая будет вероятность события A, если произошло событие B? Чтобы это узнать, вычислим условную вероятность.
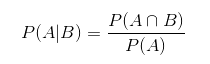
Интересно, что совместная вероятность по нескольким случайным переменным можно разделить на условные распределения по одной переменной — это преобразование называют правилом цепи:
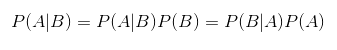
Ещё следует упомянуть правило Байеса, описывающее вероятность события, базируясь на знании условий либо других событий, связанных с главным событием:
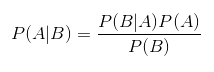
Также обратите внимание на его упорядоченную версию:
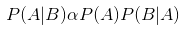
Здесь P(A) — априорная вероятность гипотезы A, а P(A|B) – вероятность гипотезы A в случае наступления события B (апостериорная вероятность). Что касается P(B|A), то это вероятность наступления события B в случае истинности гипотезы A. И, если мы говорим о машинном обучении, искусственном интеллекте либо глубоком обучении, мы, как правило, применяем правило Байеса при обновлении параметров нашей модели.
Источник: «Mathematics for Artificial Intelligence – Probability».