Устойчивость материальных систем

Устойчивость – одна из важнейших характеристик материальных систем. Под устойчивостью понимают способность системы сохранять своё состояние в условиях возмущающего воздействия среды. Исследование устойчивого и неустойчивого поведения ряда осуществляться на основе анализа поведения системы во времени после воздействия какого-нибудь возмущения.

Показатель Ляпунова характеризует степень экспоненциального разбегания соседних точек. Как хорошо известно, наличие положительного ляпуновского показателя отражает чувствительную зависимость динамической системы от начальных данных, что является одним из главных признаков детерминированного хаоса. Именно это свойство ответственно за нестабильное поведение детерминированных хаотических систем, которое часто по "внешним" проявлениям интерпретируется как случайное, на самом деле, отнюдь не являясь таковым.

С ляпуновским показателем непосредственно связан горизонт предсказуемости хаотической системы: за время, обратно пропорциональное показателю Ляпунова, система полностью теряет информацию о своём начальном состоянии. В результате, прогноз динамики хаотической системы на временах, больших горизонта предсказуемости, в принципе невозможен. Существует принципиальное ограничение на горизонт прогноза. Различные оценки времени предсказуемости T_p, в основном, сводятся к соотношению: 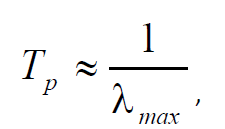где λ_max – старший ляпуновский показатель исследуемой динамической системы.

Если λ > 0. то соответствующий макроэкономический режим является локально неустойчивым и хаотическим. Если λ = 0, то говорят, что режим является нейтрально устойчивым. Если λ < 0, то режим является устойчивым и периодическим.

Часто для оценки старшего показателя Ляпунова применяют метод Бенеттина. Пусть имеется некоторая точка , которая принадлежит x₀ аттрактору А исследуемого ряда. На данную точку оказывается воздействие, которое обозначается ℇ, такое, что выполняется равенство ||X̌₀ – X₀||= ℇ. Точка X̌₀ – это точка, в которую переходит X₀ под воздействием смещения ℇ. Спустя какое-то время T происходит сравнение точки, находящейся на старом аттракторе, с точкой, находящейся на новом аттракторе, который образовался под воздействием смещения.

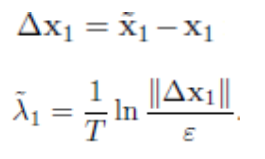Затем эта операция по расчету λ повторяется М раз. После чего высчитывается среднеарифметическая λ. Полученный результат будет оценкой старшего показателя Ляпунова. Очевидно, что для лучших оценок λ следует брать как можно больше значение М. Данный метод достаточно прост в применении к оценке старшего показателя Ляпунова, однако точность получаемой оценки λ сильно зависит от длины ряда и от количества замеров.

Хотите знать больше? Добро пожаловать на мой Телеграм-канал!