Процессы с длинной памятью

Зависимость структуры ряда от времени играет ключевую роль при моделировании или анализе временных рядов с различным типом процесса. В задаче анализа временного ряда со сложной структурой часто применяются модели класса ARIMA(p,d,q), которые моделируют различные ситуации, встречающиеся при анализе стационарных и нестационарных рядов.

В зависимости от анализируемого ряда, модель ARIMA (p,d,q) может трансформироваться к авторегрессионной модели AR(p), модели скользящего среднего MA(q) или смешанной модели ARMA (p,q). При переходе от нестационарного ряда к стационарному значение параметра d, определяющего порядок разности, принимается равным 0 или 1, т. е. этот параметр имеет только целочисленные значения.

Обычно ограничиваются выбором между d = 0 и d = 1. Однако что будет происходить, когда параметр d будет принимать дробные значения?

Параметр d характеризует степень интегрированности ряда. Если d=0, то это означает, что ряд обладает короткой памятью. Если ряд обладает короткой памятью, то последствия какого-либо шока или воздействия извне на ряд исчезнут достаточно быстро. Если d=1, то ряд обладает бесконечной памятью. В таком случае любой шок будет оказывать бесконечно долгое воздействие на ряд. Все шоки будут учтены в динамике ряда.

Был предложен новый класс моделей ARFIMA(p,d,q), допускающий возможность нецелого параметра d. Такие ряды обладают определёнными свойствами: самоподобием, дробной размерностью, медленно спадающей автокорреляцией (по гиперболической зависимости).

В настоящее время установлено, что целочисленное дифференцирование (d=1, 2 и т. д.) уничтожает не только трендовую составляющую, но и компонент с длинной памятью, оставляя только случайные колебания с короткой памятью. Прогнозировать по ним бессмысленно, поскольку они некоррелированны. Дробное дифференцирование фильтрует только трендовую компоненту и оставляет для прогнозирования составляющую с памятью.

Процессы ARMA (p, q) и ARIMA (p, d, q) являются частными случаями процесса ARFIMA при d = 0 и d = 1 соответственно. Например, авторегрессионная модель, которая сокращённо обозначается AR порядка р, может быть представлена в следующем виде:

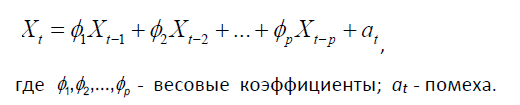
В нестационарном случае модель ARIMA (p, d, q) можно представить в виде:

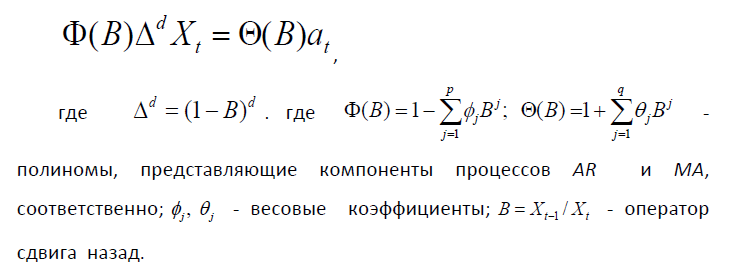
Модель ARFIMA позволяет описывать поведение рядов с длинной памятью за счёт добавления в модель класса ARIMA дробного параметра d. Решение задач на прогнозирование значений рядов с долгой памятью прогнозирования динамики ряда сводится к поиску параметров (p,d,q) в модели ARFIMA.

Хотите знать больше? Добро пожаловать на мой Телеграм-канал!