В программировании и реальной жизни полно ситуаций, при которых нет никакой необходимости вникать в глубины решаемых задач. Все ясно при первом же рассмотрении темы. Но случается и так, что требуется подтвердить или опровергнуть выражение. Здесь в силу вступает так называемая логика высказываний.
Соответствующий момент играет важную роль не только в жизни, но и в науках. Пример – математика, программирование, психология. Можно использовать разнообразную логику высказываний для подтверждения и опровержения результатов. Обо всем этом будет рассказано далее.
Понятие логики
Логические утверждения – это не просто словосочетание. Логика является целой наукой. Ее изучение помогает правильно и здраво рассуждать. Благодаря этому, человек или устройство смогут делать грамотные выводы, опираясь на рассуждения.
При рассмотрении того или иного вопроса, человек будет на основе заключений логического характера строить гипотезы. В конце 19 века математики смогли перевести процесс осмысления в понятную форму – математическую. Такие логические «высказывания» стали носить название символических.
Все современные устройства базируются на операциях логического характера. За счет них происходит обработка и совершение тех или иных манипуляций.
Виды выражений
С помощью логических операций можно строить теории, а также решать сложные задачи, результатом которых окажется справедливый итог. Стоит помнить о том, что прослеживать имеющиеся связи для анализа необходимо крайне внимательно. А еще – учитывать заданные условия, которые относятся к поставленной задаче.
Логические выражения могут быть:
- простыми;
- сложными.
В первом случае результатом обработки заданной операции выступать только «истина» или «ложь». Во втором – или итогом становятся или только истинные операции, или исключительно ложные.
Процедуры получения сложного выражения из нескольких простых имеют определенное название. А именно – формулы логического характера.
Основные операции
Математика, информатика, программирование и другие науки немыслимы без анализа, а также построения теорий по заданным вопросам. Здесь без мышления логического характера не обойтись. Соответствующий момент активно применяется в приложениях — не только сложных, но и элементарных.
Чтобы понять, как работает логи ческая цепочка в калькуляторах истинности, стоит запомнить ключевые операции над логическими выражениями. Всего их несколько:
- конверсия;
- дизъюнкция;
- конъюнкция;
- строгая дизъюнкция;
- импликация;
- эквивалентность.
В программировании также стоит обратить внимание на запись исключающего или. Это – операция XOR.
Порядок обработки
При изучении формулы логики заданных высказываний стоит запомнить порядок (приоритет) обработки операций в сложном выражении. Выполняются манипуляции так:
- инверсия (логическое отрицание);
- конъюнкция (логическое умножение);
- дизъюнкция (логическое сложение);
- импликация;
- эквивалентность.
Для того, чтобы изменить прописанный порядок выполнения обработки данных, необходимо в логических выражениях использовать скобки.
Таблицы и операции
Построить таблицу истинности можно без онлайн калькуляторов. Для этого достаточно запомнить, как работает каждая из перечисленных выше операций. У математиков с этим проблем не возникает – они хорошо заучивают предложенную далее информацию.
Конъюнкция
Носит название «логическое И» или «умножение». Часто встречается в программировании. В языках «создания контента» обладает особым обозначением. Примеры записи:
- И;
- AND;
- &;
- &&.
Выражение логического характера при конъюнкции является истиной, только когда оба простых высказывания тоже выступают в качестве правды. Если хотя бы одно из них – ложь, то вся операция примет значение False.
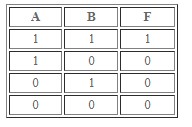
Выше представлена таблица истинности при операции конъюнкции.
Дизъюнкция
Является сложением. У этого логического выражения есть иное название – «логическое ИЛИ». Тоже встречается в программировании довольно часто.
Может иметь такие формы записи:
- ||;
- ИЛИ;
- OR;
- |.
Преобразование последовательности будет осуществляться по принципу: выражение – истина, если хотя бы одно из его составляющих – правда. Ложно, когда оба элемента имеют значение FALSE.
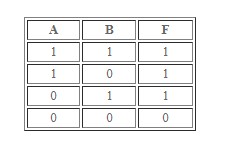
Выше – примеры таблицы истинности, которая работает в отношении дизъюнкции.
Инверсия
Следующий момент, на который стоит обратить внимание – это инверсия. Носит название «отрицание» или «логическое НЕ».
Обозначения в программировании:
- НЕ;
- !;
- NOT.
Логическое выражение при отрицании обладает следующими особенностями:
- Когда исходные данные истины, то результатом станет ложь.
- Если операция обладает значением «ложь», ее отрицание получит «истину».
- Можно рассматривать соответствующую манипуляцию как трактовку «Неверно, что…»
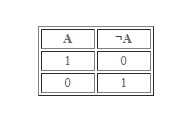
Вот такую таблицу истинности можно построить относительно инверсии.
Импликация
При любом логическом выводе стоит опираться на предлагаемые примеры и таблицы. Импликация – это следование.
В любом заданном логическом выражении результат – это истина всегда. Исключение – когда из правды следует ложь. Она связывает два высказывания (a и b), где:
- A – это условие, первое выражение;
- B – следствие.
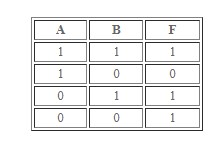
Если из A может следовать B, значит операция выдаст в результате обработки «истину».
Эквивалентность
Так называют равнозначность. Новое высказывание истинно тогда, когда оба простых выражения – это правда.
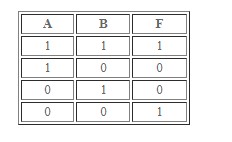
Выше – пример расчетов формулы логики заданных высказываний при эквивалентности.
Исключение
Онлайн калькуляторы могут помочь построить график или указать, что верно, а что нет, без вдумчивости в поставленную задачу со стороны пользователя. Но программистам приходится прописывать принципы функционирования и выполняемые операции вручную. Для них особенности алгебры логики и информатики крайне важны.
Порядок выполнения логических операций ранее был рассмотрен. Осталось понять, как работает исключение.
Согласно установленным правилам, операция будет истиной, когда среди значений переменных A и B есть одно правдивое. Если оба – это действительность, упомянутый принцип работать не будет.
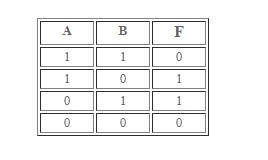
Исключающее ИЛИ – преобразование, которое носит название «сложение по модулю два».
Законы алгебры логики
Формулы логики высказываний запомнить не так трудно. Но учить соответствующие законы – не всегда оправданный шаг. Для выполнения операций достаточно вспомнить алгебру, а также преобразование выражений.
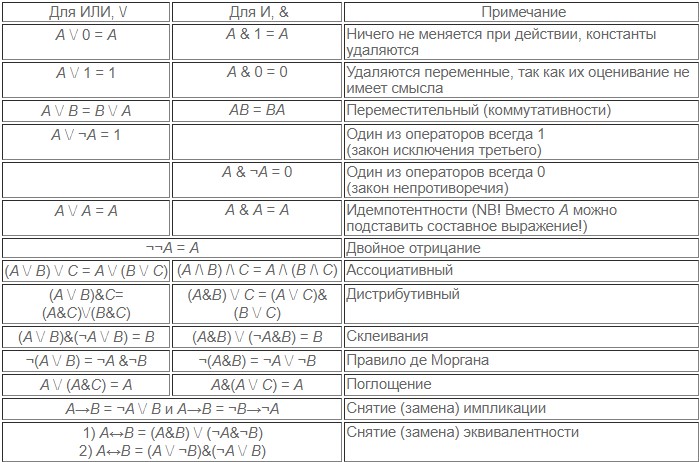
Выше – примеры логических операций, упрощенные для запоминания человеком.
Чтобы лучше понять тему
В сети сделано и размещено немало калькуляторов, при помощи которых можно судить об истинности высказываний. Но хороший программист должен самостоятельно уметь производить соответствующие подсчеты. Операцией логического характера не является выражение, результатом которого не выступает:
- понимание смысла;
- изменение содержания или объема;
- образование новых понятий.
Логическое выражение в программировании обычно предусматривает работу с операторами:
- XOR;
- IF;
- IF…Else.
А для того, чтобы лучше понимать соответствующую тему, рекомендуется пройти онлайн курсы дистанционно. Они помогут быстрее вникнуть в особенности программирования, коддинга и выбранных языков. По выпуску ученику будет выдан сертификат, указывающий на наличие знаний в выбранном направлении. Так логическое выражение и упомянутые ранее операции не доставят никаких хлопот даже новичку-разработчику.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:







