При изучении алгоритмов и структур данных нередко поднимается тема сортировки элементов данных. Если говорить честно, необходимость в реализации какой-нибудь уникальной сортировки при работе со связанными структурами данных возникает довольно редко, а то и не возникает вовсе. Дело в том, что в современных языках программирования для этих целей существуют свои оптимизированные методы (тот же array.sort() в JavaScript). Так зачем же изучать данный вопрос? Дело в том, что это хороший пример как алгоритмов, так и баланса между расходом памяти и времени. В этой статье мы рассмотрим 2 самых популярных метода сортировки с разным расходованием ресурсов: Bubble Sort и Merge Sort. Для примера будем использовать язык программирования JavaScript.
Bubble Sort
Идея заключается в том, чтобы, выполняя проход массиву, находить элемент с наибольшим значением, одновременно с этим «протаскивая» его в конец. Если учесть, что за одну операцию обхода мы «дотаскиваем» лишь 1 максимальный элемент, чтобы реализовать Bubble Sort, нам надо будет выполнить n-операций по обходу (здесь n — это длина массива). Таким образом, мы получаем квадратичную алгоритмическую сложность O(n^2).
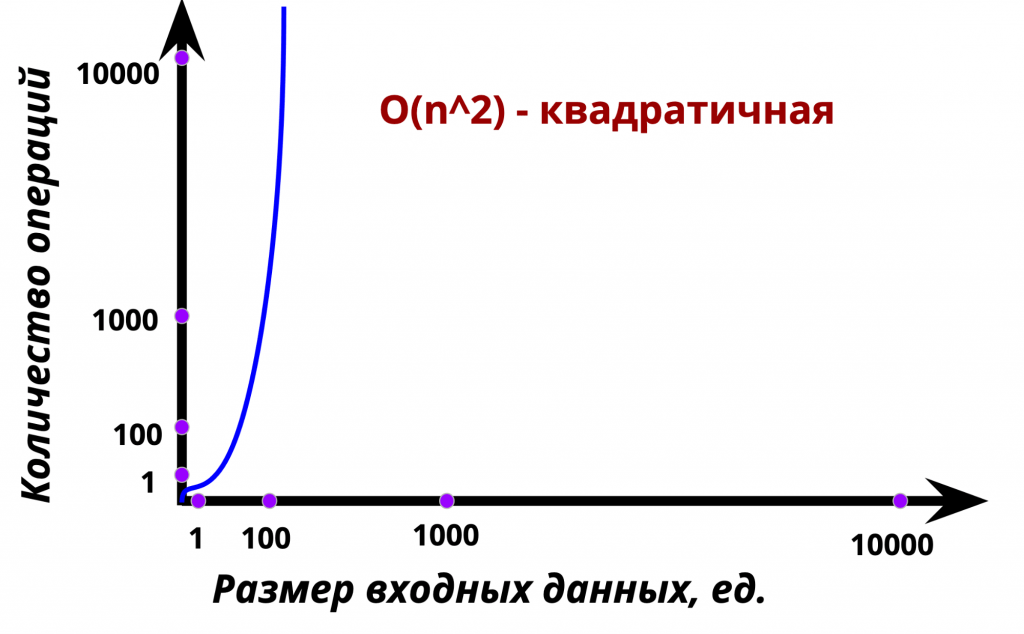
Но до того как погрузиться в реализацию, давайте сначала рассмотрим визуализацию описанного выше процесса:
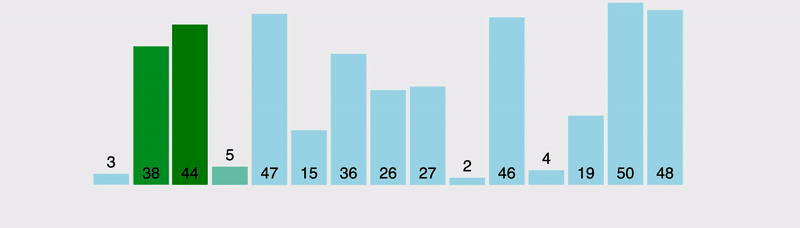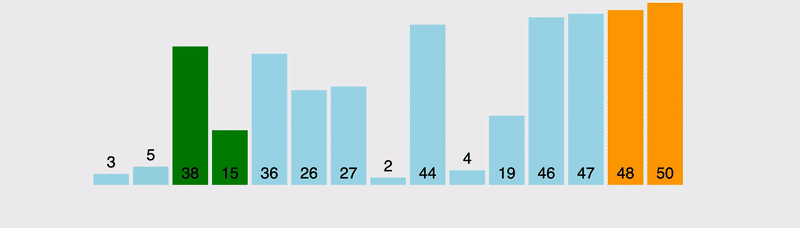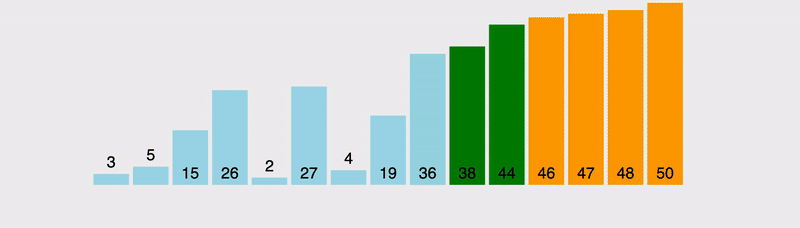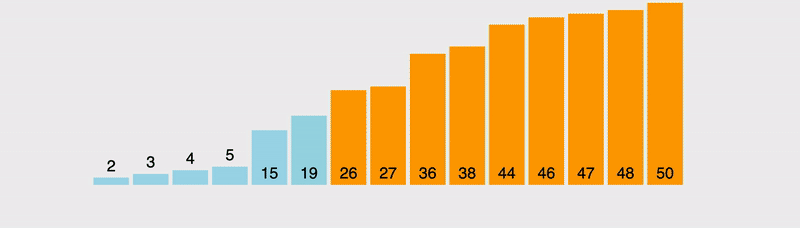
То есть суть работы весьма проста, и заключается она в прохождении по массиву, определении значения текущего и последнего элементов, их сравнении и распределении. Когда левый компонент больше правого, они меняются местами, после чего для сравнения берется следующий компонент. В результате мы или постоянно двигаем наибольший компонент вправо, пока он не дойдет до конца структуры данных, или, если наткнемся на компонент с бОльшим значением, перемещаемся дальше по распределенной структуре, причем последующие операции будут уже считаться связанными с новым наибольшим значением.
Теперь реализуем это в коде:

Может, применение Bubble Sort с ее аж квадратичной алгоритмической сложностью не так уж и практично, ведь есть и более универсальные решения, связанные с сортировкой данных? На деле все не так просто, ведь вышеописанный метод имеет одно существенное преимущество — расход памяти. Для смены мест 2-х элементов нам понадобится только одна вспомогательная переменная, в результате чего мы получаем константную сложность по памяти. А это огромный плюс, если сравнивать с сортировкой слиянием, которую мы сейчас рассмотрим.
Merge Sort
Вот, как она выглядит:
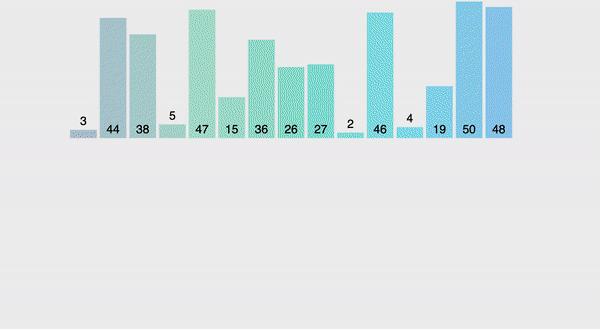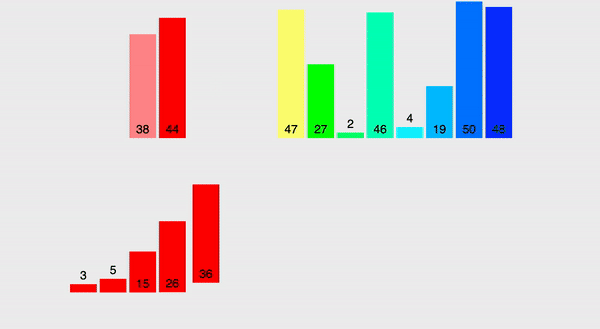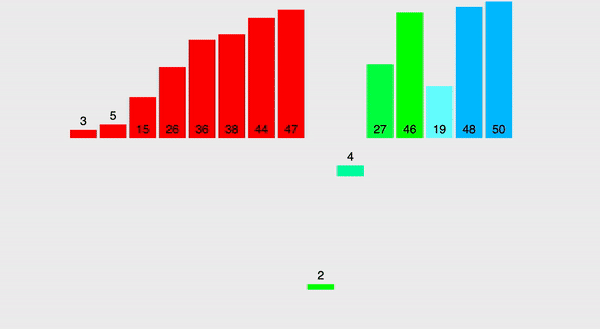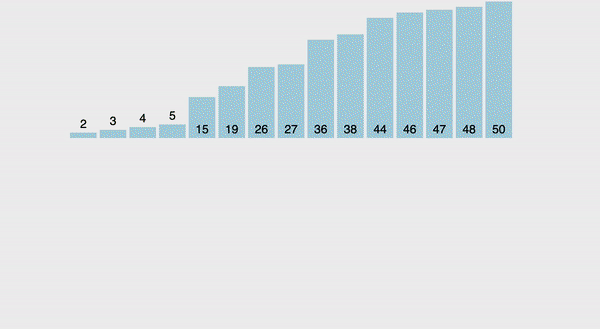
Глядя на гифку в первый раз, бывает сложно понять, как происходит распределение элементов. Идея тут следующая:
- Разбить структуру данных пополам на 2 новых массива.
- Разбить каждую половину снова пополам, потом опять пополам и так до тех пор, пока не останутся массивы, содержащие лишь 1 элемент.
- Выполнить операцию обратного слияния (попарно), но уже сортируя компоненты по возрастанию.
Из-за постоянной разбивки и попарного слияния алгоритмическая сложность используемой процедуры составляет O(n * log n).
Смотрим на основной код:
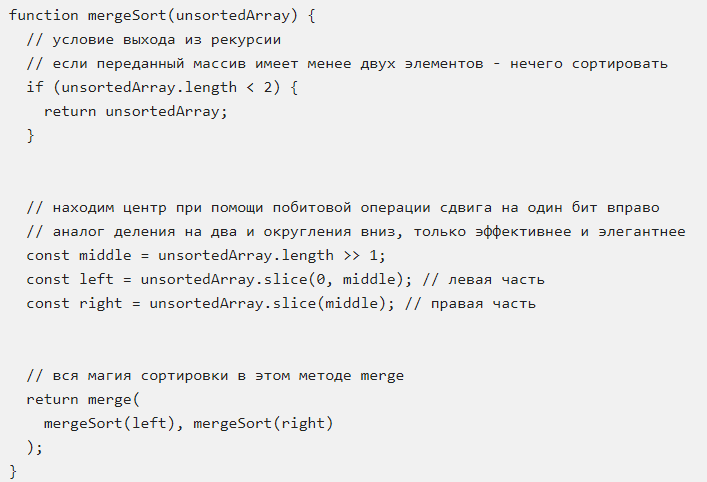
Посмотрите на картинку ниже, представляющую собой очередную визуализацию процесса, где прекрасно видно, как именно происходит разбивка и последующее обратное попарное слияние.

В чем же логика? Смотрите, к нам «приходят» два массива: правый и левый. Оба или уже отсортированы, или просто включают в себя лишь 1 компонент. Далее надо начинать обходить обоих (потребуется лишь один обход с 2-мя указателями: первый укажет на итерируемый компонент левого массива, второй — на компонент правого), причем брать — наименьший из 2-ух элементов, забрасывая его в новую структуру, которую мы и возвратим как отсортированную.
Вот наш код:

Теперь должно быть все понятно.
Последнее, о чем стоит сказать, — достаточно до конца пройти хотя бы один Array, потому что оставшиеся непройденные значения будут однозначно больше, в итоге их нужно будет просто добавить в конец (в коде это реализуется тоже в конце, где сливаются остатки с помощью метода concat.)
Вывод прост: более быстрая сортировка потребует существенно больше памяти. Также можно сказать еще кое-что: Bubble Sort и Merge Sort — это, по сути, одни из лучших универсальных методов сортировки. А все потому, что они стабильно работают практически в любых случаях и с любыми данными (в пределах разумного). Да, есть методы, выигрывающие по алгоритмической сложности, к примеру, Radix Sort. Но практическое использование подобных методов специфично, поэтому их вряд ли можно назвать универсальными.
Несколько советов
Парочка полезных рекомендаций:
- совсем не обязательно наизусть знать все структуры данных и алгоритмы;
- самые нужные в плане пользы знания, чаще всего являются наиболее простыми в плане освоения;
- не надо помнить все реализации — все мы люди, поэтому какие-то реализации можно и забыть. Но на практике вам будет достаточно 1 раз в них разобраться и иметь представление об их возможностях;
- анализируйте свои алгоритмы. Надо задумываться над их эффективностью — это полезно;
- чем более эффективный код вам удается создавать, тем более высокую производительность и надежность будет демонстрировать ваш программный продукт (как следствие — тем более крутым разработчиком вы будете).
По материалам: https://dou.ua/lenta/articles/what-you-should-know-about-algorithms/.
Какие еще статьи можно дополнительно почитать на тему структур данных:
— «Понятие структуры данных для программиста. Массивы»;
— «Топ-8 структур данных для программиста»;
— «Дерево как структура данных. Двоичные деревья».
Изучив эти статьи, вы будете знать, что такое структуры данных, зачем они используются, как происходит распределение данных в зависимости от структуры, какие операции поддерживаются, что такое графы, деревья, боры и связные списки, какое значение имеет словосочетание first out, как обратиться к элементу в списке и т. д.







