Мы уже рассказывали про алгоритмы, их виды и свойства. В этой статье поговорим о том, как составить алгоритм решения какой-нибудь задачи, что и в какой последовательности следует написать.
При решении задач на алгоритмы немаловажным является умение использовать язык блок-схем. Процесс решения одной и той же задачи можно реализовать посредством применения алгоритмов разных классов, поэтому результат может отличаться и по времени счета, и по объему вычислений, и по сложности. Записывая алгоритмическую последовательность с помощью составления блок-схем, вы сможете сравнить решения, выбрав самый лучший algorithm. Также появляется возможность упростить способ решения, найти и устранить ошибку.
Можно ли отказаться от языка блок-схем при описании алгоритма и сразу составить его на языке программирования? Можно, однако существует риск выбора неоптимального решения и существенных потерь времени. Именно поэтому при данной постановке вопроса рекомендуется сначала составлять способ решения задачи путем создания блок-схемы, а уже потом переводить алгоритм на нужный язык программирования.
Когда речь идет о задаче высокого класса сложности, не обойтись без пошаговой реализации. Сначала продумывают общую структуру алгоритмической последовательности, то есть детальная проработка отдельных частей здесь не требуется. Модули, которые далее потребуют более детального рассмотрения, обводят пунктиром, чтобы потом продумать и детализировать.
В решении задачи на алгоритмы выделяют ряд этапов:
- Математическое описание.
- Определение входных/выходных данных.
- Разработка алгоритма по решению поставленной задачи.
Алгоритмические конструкции базовых классов
В теории программирования считают, что для того, чтобы составить запись любого, даже самого сложного алгори тма, хватит 3-х базовых структур. Речь идет о следующих алгоритмах:
- линейного класса;
- ветвления (речь идет о разветвляющихся алгоритмах);
- циклического класса.
Алгоритмы линейного класса
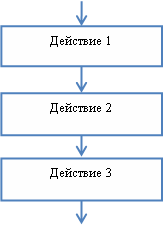
Образуются из последовательности действий, которые следуют одно за другим. К примеру, чтобы определить площадь прямоугольника, надо сначала задать длину 1-й стороны, потом — 2-й стороны, ну а в конце уже можно решать пример по формуле нахождения площади.
В качестве примера возьмем задание с разработкой алгоритма по вычислению гипотенузы прямоугольного треугольника, зная длины катетов a и b. Вспоминаем вышеописанные этапы разработки:
1. Математическое описание.
Математически задача решается по следующей формуле:
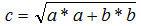
Здесь c является длиной гипотенузы, a, b – длинами катетов.
2. Определяем входные/выходные данные.
Входные данные — значения катетов a и b. Выходные — длина гипотенузы c.
3. Разработка алгоритма.
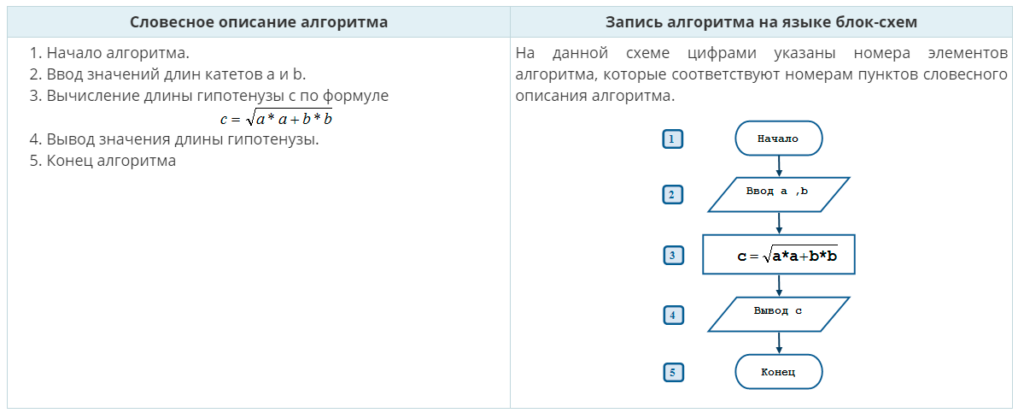
Алгоритмы ветвления
В таких алгоритмических последовательностях всегда существует какое-нибудь условие. В зависимости от того, соблюдается это условие либо нет, происходит выполнение той либо иной последовательности действий.
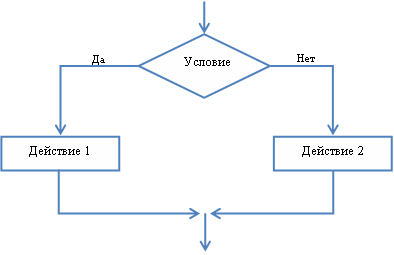
Для примера возьмем задание, постановка которого связана с разработкой алгоритма по вычислению наибольшего числа из 2-х чисел: x и y.
1. Математическое описание.
Из первых классов математики мы знаем, что когда x > y, то x больше y и наоборот, что является очевидными вещами. И если x = y, то числа равны.
2. Определяем входные/выходные данные.
Входные данные — это значения x и y. Выходными данными являются:
- самое большое число;
- любое из чисел в том случае, если они равны.
Таким образом, чтобы решить эту задачу на алгоритмы, надо знать значения переменных x и y.
3. Разработка.
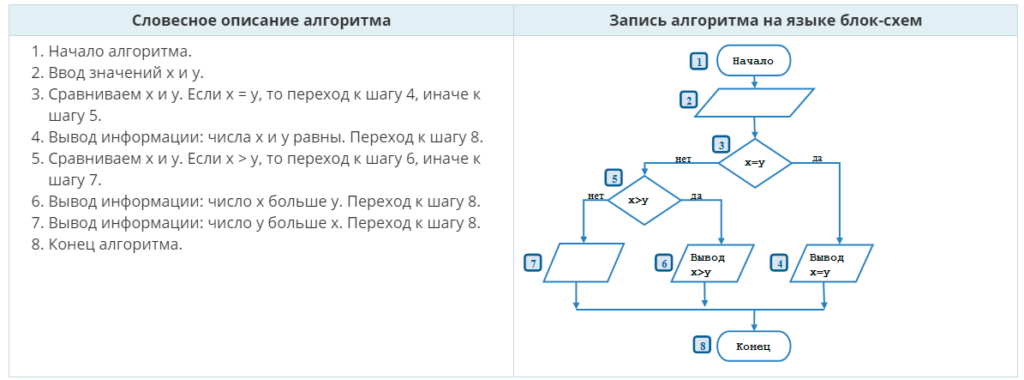
В вышеуказанной схеме цифрами отмечены номера алгоритмических элементов, соответствующие номерам шагов словесного описания. Здесь есть 3 ветви решения:
- 1, 2, 3, 4, 8;
- 1, 2, 3, 5, 6, 8;
- 1, 2, 3, 5, 7, 8.
Алгоритмы циклического класса
В алгоритмах циклического класса некоторая часть действий из задания повторяется до тех пор, пока не нарушится заранее определенное условие. Выполнение условия проверяется в начале. Совокупность операций, которые выполняются многократно, — это тело цикла.
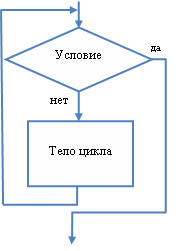
В алгоритмических последовательностях этого класса выделяют ряд понятий:
- параметр цикла (с изменением этой величины связано многократное выполнение цикла);
- начальное и конечное значения циклических параметров;
- шаг цикла (речь идет о значении, на которое меняется параметр при каждом повторе).
Работу циклов организуют по специальным правилам. Алгоритмическая последовательность циклического класса включает в себя и подготовку, и тело, и условия продолжения работы.
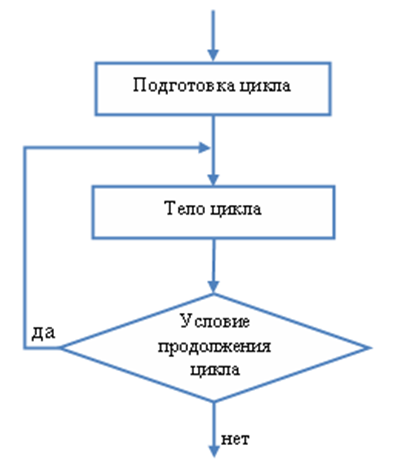
В подготовку входят действия, которые связаны с заданием исходных значений:
- начальные значения;
- конечные значения;
- шаг.
В тело цикла входят:
- многократно повторяющиеся операции по вычислению искомых величин;
- подготовка последующего значения параметра;
- подготовка иных значений, нужных для повторного выполнения действий непосредственно в теле.
В условии продолжения цикла определяют допустимость выполнения повторяемых операций. Когда циклический параметр равен либо превышает конечное значение, выполнение прекращается.
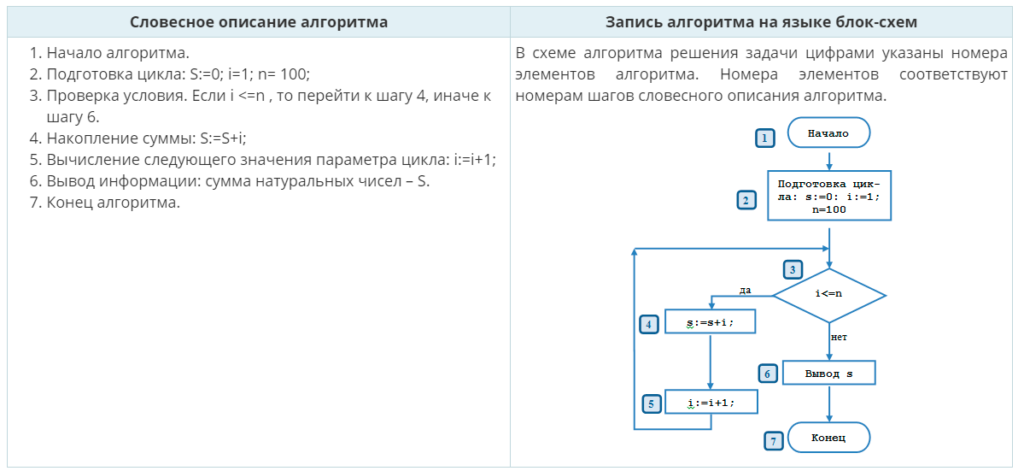
Рассмотрим задание, постановка которого связана с разработкой алгоритма вычисления суммы натуральных чисел в диапазоне от 1 до 100.
1. Математическое описание.
Сначала следует обозначить сумму натуральных чисел буквой S. В результате формулу вычисления суммы чисел от 1 до 100 можно записать следующим образом:
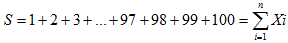
Здесь Xi является натуральным числом X c номером i. Этот номер меняется от 1 до n. А n=100 обозначает общее кол-во натуральных чисел.
2. Определяем входные/выходные данные.
Входные данные — это натуральные числа: 1, 2, 3, …, 99, 100.
Выходные данные представляют собой значение суммы членов последовательности натуральных чисел.
Относительно параметра цикла — речь идет о величине, определяющей число циклических повторений. В нашем задании i представляет собой номер натурального числа.
Подготовка цикла — задание начального и конечного значений циклического параметра. Тут надо пояснить следующее:
- начальное значение циклического параметра равняется единице,
- конечное значение — n,
- шаг равен 1.
Чтобы обеспечить корректность суммирования, надо, чтобы начальное значение суммы предварительно равнялось нулю.
Тело цикла. В теле станут выполняться как накопление значения суммы, так и вычисление последующего значения циклического параметра по формулам ниже:
- S=S+i;
- I=I+1.
Циклическое повторение должно осуществляться до тех пор, пока не добавится последний член последовательности натуральных чисел, то есть до тех пор, пока циклический параметр будет меньше либо равен окончательному значению параметра.
3. Разработка.
Вводим следующие обозначения: S – это сумма последовательности, i – это значение натурального числа.
Начальное циклическое значение i=1, конечное — i =100, шаг равен 1.
По материалам: https://www.turbopro.ru/index.php/osnovy-programmirovaniya/6836-algoritmy-razrabotka-algoritma-resheniya-zadachi.






