Важное условие хранения данных в памяти ПК — возможность преобразования этих данных в форму, которая понятна компьютеру. Не менее важно подобрать структуру, которая будет подходить для конкретных типов данных, то есть предоставит исчерпывающий набор возможностей для работы с имеющейся информацией. Именно для этого следует знать основные структуры данных и уметь с ними работать. Вдобавок к этому, важно понимать, что структуры данных — важнейшая часть разработки программ и одна из самых распространенных тем на собеседованиях. В этой статье мы расскажем о десяти наиболее распространенных структурах, большинство их которых очень хорошо известны.
Связные списки и массивы
Связный список нередко сравнивают с массивом, ведь многие другие структуры данных можно реализовать или посредством массива, или посредством связного (связанного) списка. Хотя и массив, и список, имеют свои плюсы и минусы.
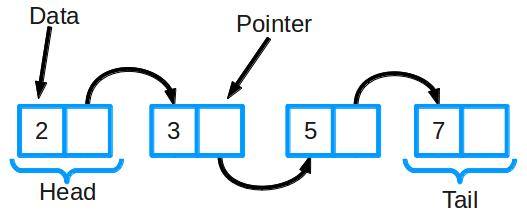
Связный список — это группа узлов, вместе представляющих собой последовательность. Каждый такой узел включает в себя:
— фактические данные, которые хранятся;
— ссылку-указатель на следующий в последовательности узел.
Также выделяют дважды связанные списки, где каждый узел имеет указатель как на следующий элемент в списке, так и на предыдущий.
Основные операции:
- добавление элемента;
- удаление элемента;
- поиск в списке.
Отдельное внимание стоит уделить массивам — это структуры данных, обеспечивающие хранение элементов, имеющих схожий тип данных. Такие элементы находятся в смежных местах памяти (каждый элемент массива — в своей ячейке). Общее число элементов в массиве характеризует его длину. Доступ к данным массива осуществляется по позиции конкретного элемента, для чего используется ссылка, называемая индексом массива.
Особенности массива:
- элементы находятся в смежных ячейках памяти;
- индекс меньше, чем общее число элементов;
- переменная, объявленная в качестве массива, способна хранить несколько значений;
- практически любой язык программирования одинаково понимает массив, однако может по-разному его объявлять и инициализировать, то есть решения в программном коде могут отличаться реализацией.
Массивы способны иметь разное количество измерений. Вот как выглядит одномерный массив:

Массив a имеет только одну строку и размер 16 ячеек. Доступ к элементу осуществляется по индексу, причем максимальный индекс равняется 15, так как нумерация начинается с нуля.
Бывают массивы с двумя измерениями (двухмерные), тремя (трехмерные) и т. п., то есть они могут быть n-мерными. Двумерный массив уже можно назвать матрицей. Доступ к элементу такой матрицы уже будет осуществляться по i-й строке и j-м столбце — a[i][j].

Кратко о том, зачем вообще нужны массивы:
- массивы — хорошее решение, если надо хранить в одной переменной несколько значений;
- в такой структуре проще и быстрее обрабатывать однотипные данные, выполнять поиск и сортировку.
На практике в программировании чаще используют в качестве структур данных одномерные и двумерные массивы.
Стеки
Стек напоминает стопку, содержащую книги или учебники: если нужна книга из середины, надо сначала взять те книги, которые находятся сверху. То есть это структура данных, при работе с которой можно вставлять либо удалять элементы только в начале. Последний добавленный элемент является первым, который из этого стека выходит (Last In First Out — LIFO), то есть компоненты добавляются и удаляются лишь с одного конца — так называемой вершины стека.

Очереди
Просто вспоминаем очередь в продуктовом гипермаркете. Тот, кто стоит первым, первым и обслуживается.

Но эта структура данных, в отличие от предыдущей, организована по принципу First In First Out (FIFO). Элементы добавляются с одного конца (enqueue), а удаляются с противоположного (dequeue). Кто первый пришел, первый и уйдет (будет «обслужен на кассе»).
Множества
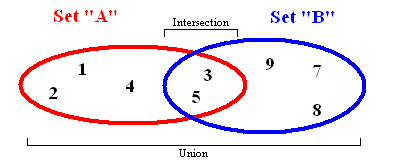
С помощью множеств данные хранятся без определенного порядка, а также, что немаловажно, без повторяющихся значений. Элементы можно добавлять, удалять, объединять, создавать подмножества и т. д.
Map
Структура, хранящая данные в парах ключ-значение, причем каждый ключ в такой структуре является уникальным. Другое название — словарь или ассоциативный массив. Неплохое решение для быстрого поиска данных.
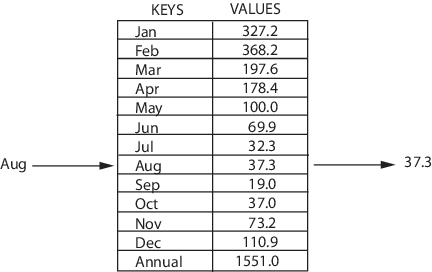
Можно добавлять/удалять пары из коллекции, менять уже существующие пары, искать значения, связанные с конкретным ключом.
Хэш-таблицы
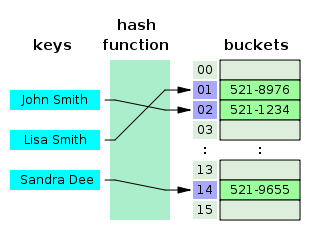
Эта структура реализует интерфейс map, который, как и в предыдущем случае, позволяет хранить пары ключ-значение. Для вычисления индекса в массиве данных используется хэш-функция. Подробнее о хэш-функции и алгоритме хэширования можете почитать в этой статье.
Двоичное дерево поиска
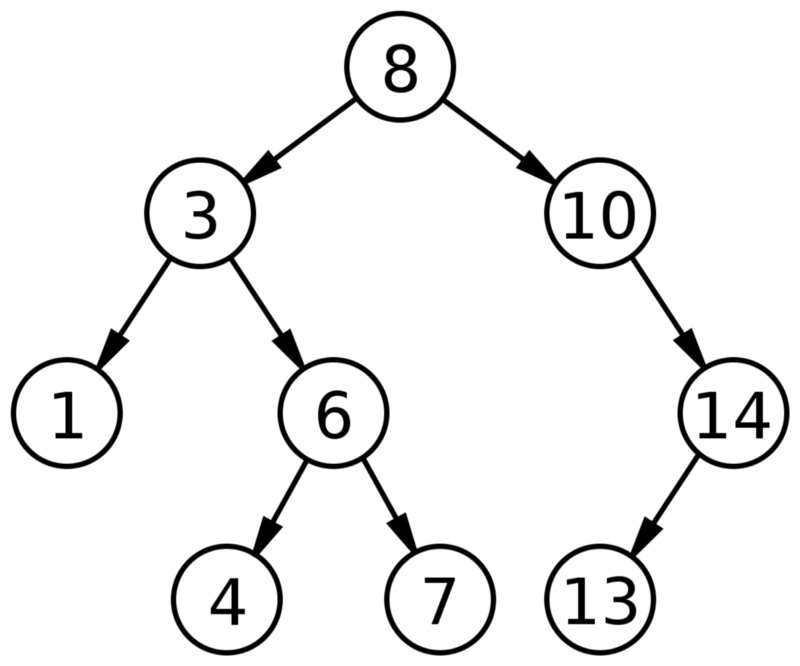
Дерево (древо) представляет собой структуру данных, состоящих из узлов, причем:
- У каждого дерева есть корневой узел (расположен сверху).
- У каждого корневого узла есть 0 и более дочерних узлов.
- У каждого дочернего тоже есть 0 и более дочерних узлов и так далее.
Двоичное дерево обладает двумя дополнительными свойствами:
- У каждого узла — до 2 потомков (детей).
- Для каждого узла значения левых потомков меньше значения текущего узла и меньше значения правых потомков.
Двоичные деревья поиска используются для быстрого нахождения, добавления или удаления элементов.
Префиксное дерево
Дерево префикса — дерево поиска. Данные хранятся в шагах, каждый из шагов — узел. Благодаря возможности быстрого поиска и наличия функции автоматического дописывания, префиксное древо часто применяют при хранении слов.
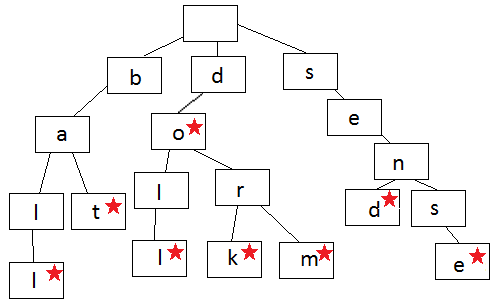
Каждый узел — это одна буква слова. Чтобы записать слово, надо следовать ветвям. На картинке выше содержатся следующие слова:
Двоичная куча
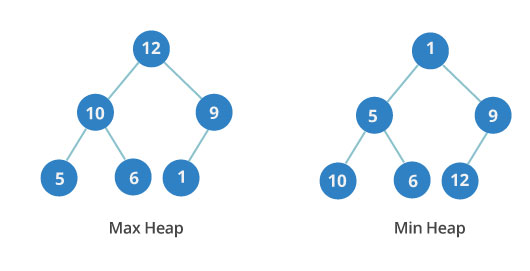
Двоичная куча — тоже дерево с узлом, в котором не больше двух детей. Оно характеризуется полнотой — все уровни заполнены полностью, причем последний заполняется слева направо. Бывает минимальным либо максимальным.
Графы
Это совокупности узлов, называющимися вершинами, и ребер (связей между этими вершинами). Еще графы называют сетями. Понять суть можно, вспомнив социальную сеть в интернете. Вершины — это люди, ребра — дружеские связи между людьми.
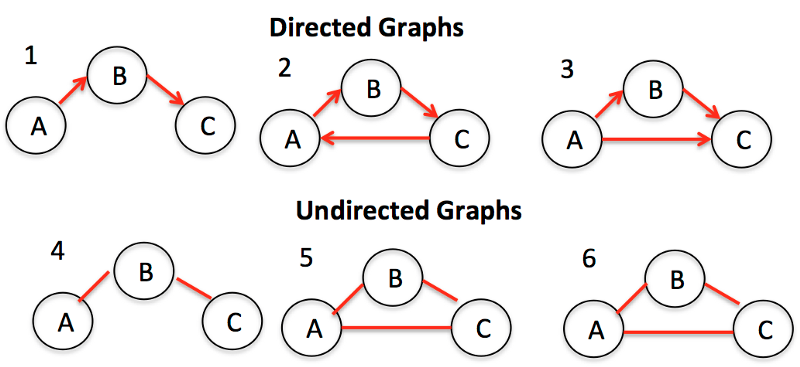
Графы бывают:
— ориентированными (с направлением);
— неориентированными (без какого-нибудь направления на ребрах между вершинами).
Частные способы представления графа — матрица смежности и список смежности.
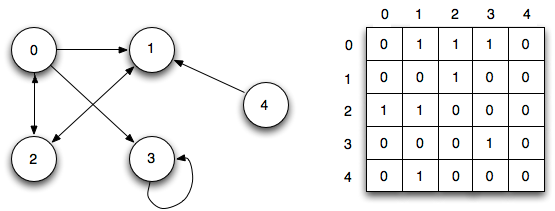

Источник: https://www.freecodecamp.org/news/10-common-data-structures-explained-with-videos-exercises-aaff6c06fb2b/.
Нашли ошибку во время чтения материала? Пишите комментарий!




