Матрица – это своеобразный математический объект, который записывается в виде таблицы элементов. Обычно представлен прямоугольником или квадратом. Математический объект, который записывается в виде таблицы компонентов, состоящей из определенного количества строк и столбцов.
С соответствующими составляющими можно выполнять разные действия. Пример – решать уравнения. Именно об этом пойдет речь далее. Информация пригодится как математикам, так и сотрудникам IT-сферы.
Матричное уравнение – это…
Матричное уравнение – это уравнение, которое напоминает линейный (числовой) аналог. Но в качестве элементов в нем используются матрицы.
Типовое уравнение подобного характера включает себя ранее упомянутые математические объекты, а также некоторую неизвестную матрицу X. Именно ее и необходимо вычислить.
Что потребуется для обнаружения результата
Для того, чтобы найти значение неизвестного, которое содержит уравнение, каждый должен сначала тщательно изучить теорию. Без этого проводить необходимые манипуляции не получится.
Решить матричное уравнение можно, если заучена следующая теория:
- понятие соответствующего объекта и его составляющих;
- определитель матрицы;
- ключевые операции над рассматриваемыми компонентами;
- определение столбцов матрицы, главной диагонали;
- что такое транспонированная матрица.
Также человек должен уметь решать линейные числовые уравнения. Без всего этого смысл изначально поставленной задачи теряется.
Сложение и вычитание
Для того, чтобы должным образом можно было решить пример, содержащий матричные компоненты, необходимо хорошо разбираться в элементарных операциях с ними. Первый вариант – сложение и вычитание.
Стоит запомнить – решать задачи по сложению удастся лишь матрицы одного и того же размера. Результатом станет математический объект аналогичного «объема».
Сам процесс вычислений достаточно прост – нужно сложить или вычесть соответствующие элементы в столбцах и строках.
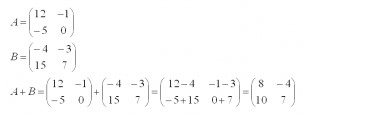
Выше – наглядный пример сложения. Вычитание производится аналогичным образом.
Умножение на число
Матрицы можно умножать на то или иное число. Такая манипуляция с легкостью производится любым математиком. Решение задачи напоминает линейные примеры.
Здесь необходимо запомнить следующие данные:
- операции подобного плана возможны с матрицами любого размера;
- для получения результата на необходимое число нужно умножить каждый элемент упомянутого мат объекта;
- полученный результат – матричный компонент аналогичного размера.
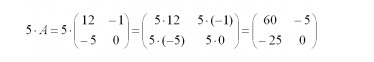
Выше – наглядный пример того, как осуществляется умножение на число 5.
Перемножение друг с другом
Умножение матриц между собой – манипуляция, которую можно осуществлять не всегда. Пример – даны мат объекты A и B. Их удастся перемножить, если количество столбцов матрицы a будет равно строкам матрицы b.
Каждый компонент, получившийся в ходе расчетов, стоящий в i-строке и j-столбце равен сумме произведений соответствующих элементов в i-строчке первого множителя и j-столбце второго.
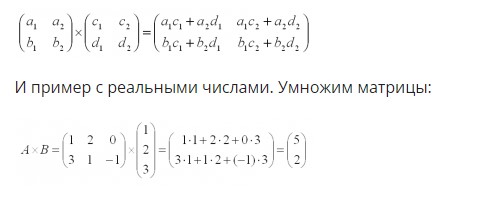
Данный шаблон и наглядный пример помогут найти грамотное решение при перемножении матричных объектов.
Транспонирование
Математика – наука, в которой формулы матриц и иных составляющих играют важную роль. Если не усвоена теория, решить поставленную задачу не получится. Для уравнений может потребоваться транспонированная ма трица.
При транспонировании строки и столбцы будут меняться местами. На письме такие компоненты обознаются как AT.
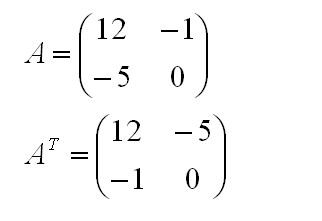
Это – наглядный пример того, как осуществляется соответствующая математическая операция.
Определитель
В случае с определителем необходимо уяснить следующие данные:
- определитель – это детерминант;
- представляет собой численную характеристику квадратной матрицы;
- при помощи определителя удастся решить множество математических задач;
- для нахождения соответствующего результата необходимо вычислить разность произведение составляющих главной и побочной диагоналей.
Определитель матрицы первого порядка (это – единичные матрицы) будет равен этому самому компоненту. Если речь идет об объекте размером 3×3, ситуация усложняется.
Для нее значение детерминанта будет равно сумме произведений компонентов главной диагонали и произведений составляющих на треугольниках с гранью параллельной главной. От последней нужно отнять произведение элементов побочной диагонали и произведение чисел, лежащих на треугольниках с гранью параллельной побочной диагонали.
На практике вычисление детерминантов больших размеров встречается редко. Некоторые, чтобы не запутаться, для решения поставленной задачи пользуются разнообразными онлайн калькуляторами. Их смысл – объяснение вычислительного процесса, а также выдача грамотных результатов.
Обратная матрица
Для каждого числа a, которое не равно нулю, существует обратное a-1. Оно будет таким, что произведение оных на выходе даст единицу. Формула записи проста: a*a-1=1. Это понятие подходит и для квадратных матриц.
Матрица A-1 будет обратной по отношению к матрице A, если при умножении оной на данную, как справа, так и слева, получится единичная матрица. К таковым относят математические объекты, включающие в себя всего один элемент (то есть, одну строку и столбец).
Не каждый квадратный матричный элемент имеет обратную матрицу. Если a не равно нулю – это достаточное и необходимое условие существования a-1, то для существования A-1 соответствующим требованием будет |A| не равен нулю.
Миноры и дополнения
Для полного понимания теории, связанной с матрицами и уравнениями, нужно разобраться с понятием алгебраических дополнений, а также минором:
- Если в определителе n-го порядка происходит вычеркивание i-строки и k-столбца, на пересечении которых расположен объект aik, то полученный детерминант (n-1)-порядка будет обозначаться минором Mik.

- Минор с определенным знаком, который находится в зависимости от четности суммы i+k номеров строчки и столбца, на пересечении которых расположен компонент aik, — это алгебраическое дополнение. Обозначается как Aik=(-1)i+kMik.
- Когда в детерминанте порядка n все составляющие последней строчки (столбца), за исключением компонента, стоящего в правом нижнем углу, равняются нулю, то определитель – это произведение соответствующего элемента на минор.
- Если у детерминанта все составляющие строчки/столбца за исключением одного равняются 0, то определитель – это произведение этого самого компонента на алгебраическое дополнение.
Наглядные примеры и доказательства перечисленных утверждений, раскрывающие их смысл, можно обнаружить по этой ссылке.
Уравнения и их решение
Теперь, когда уделено время произведению матрицы на число, а также иным элементарным операциям с рассматриваемыми объектами математики, можно приступать к непосредственному решению уравнений. Это не самый трудный процесс. Математика здесь находится примерно на школьном уровне.
Формула вычислений у матричных уравнений – точно такая же, как и простых алгебраических, в которых есть умножение. Здесь на помощь придет теория относительно обнаружения произведения матриц.
Пусть будут даны: A * X = B или X * A = B, где A и B – это известные матрицы, а X – неизвестная. Далее ситуация будет зависеть от конкретных обстоятельств:
- В первом случае, когда речь идет об уравнении A * X = B, обе части требуется умножить на обратную к A матрицу A-1 с левой стороны. Получится E * X = A-1 * B, где E – единичная матрица. Отсюда следует, что E * X = X. Результат вычислений – X = A-1 * B.
- Во втором случае, при уравнении X * A = B ситуация будет обстоять аналогичным образом. Но направление умножения на матрицу, обратную матрице A, меняется. Элемент B будет перемножаться с ней с правой стороны. Получится X * A * A-1 = B * A-1. Итог – X = B * A-1.
- Есть и третий случай – когда неизвестная матрица в уравнении расположена в середине произведения трех матриц: A * X * B = C. Здесь нужно известную матрицу из левой части умножить на обратную той, что стоит слева в заданном уравнении. И справа на матрицу, обратную той, что была с правой стороны. Итог будет следующим: X = A-1 * C * B-1.
Если же X в заданном примере – это обычное число, то формула обнаружения результата будет точно такой же, как и в линейных уравнениях.
Как лучше разобраться в теме
С формулой матрицы, а также ее основными компонентами теперь все понятно. И с основными операциями тоже удалось познакомиться. Отныне с легкостью найдем матрицу даже в уравнении при необходимости.
Для того, чтобы лучше вникнуть в соответствующую тему, стоит хорошенько изучить школьный курс математики, а также алгебру на 1 курсе обучения в ВУЗах. Информация пригодится как ученым, так и программистам.
Научиться коддить можно на специализированных дистанционных курсах. Они помогут быстро вникнуть в основы математики и информатики, а также создания приложений и игр. Курс рассчитан на срок до года. В процессе даже новичок, далекий от точных наук, сможет разобраться с матрицами и коддингом. А еще человек получит бесценную практику и новые полезные знакомства.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:






