Алгоритмы быстрого умножения: метод Карацубы

В этой статье будет рассмотрен алгоритм умножения по методу Карацубы и три его идеи. Дополнительно выполним оценку времени работы этого алгоритма.

Формальное описание последовательности действий, ведущих к достижению конкретной цели, называют алгоритмом. Если говорить об информационных технологиях, то здесь в качестве исполнителя выступает вычислительное устройство. Оно проверяет свойства объекта, данного на входе, с последующим вычислением значения в соответствующей системе счисления.

Алгоритм может проверить простоту входящего числа (однозначное, многозначное), выполнить необходимую операцию (сложение и умножение, деление и вычитание). Но тут интересно другое: для программиста algorithm — это идея программы, поэтому нередко для того, чтобы написать качественный программный код, нужно изучить классические алгоритмы. А вот для математика algorithm представляет собой большую формулу, позволяющую работать с числами с целью вычисления необходимых значений (умножения, деления и пр.). И алгоритм, работающий наикратчайшим способом и быстрее, чем это принято, — весьма интересный математический факт.

Говоря о кратчайших способах вычисления, возьмем для примера не деление, а умножение. Известное всем умножение в столбик 2-х n-разрядных чисел занимает n² умножений разряд на разряд. Так как происходит умножение каждого числа на каждое число, получается порядка n² сложений. Возникает вопрос: а есть ли кратчайший способ умножения? Можно ли умножать быстрее? Ранее существовала гипотеза, что кратчайшего пути не существует, т. к. это невозможно — все-таки пар цифр же n², плюс все это надо перемножить. Да и вообще, если бы существовал кратчайший способ умножения (алгоритм вычисления чисел), его давно бы уже придумали.

Однако советский ученый и математик Анатолий Алексеевич Карацуба такой алгоритм создал.

Чтобы быстро умножить два 2-разрядных числа, по определению, надо вычислить четыре произведения, а потом сложить их и вычислить перенос.

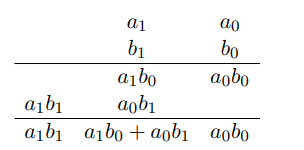
Первая идея метода Карацубы

Идея заключается в том, что 2 двухразрядных числа можно перемножить не за четыре, а за три операции умножения:

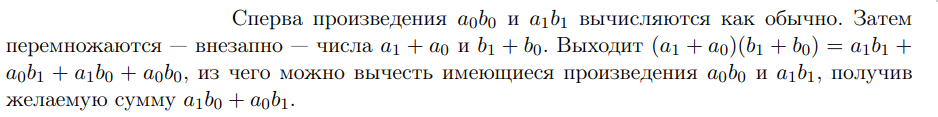
Вторая идея

Согласно ей, точно таким же образом можно умножать 2 n-разрядных числа:

Третья идея

Суть проста: чтобы вычислить каждое из 3-х произведений чисел вдвое меньшей длины, следует использовать тот же метод рекурсивно. Причем на каждом уровне рекурсии размер задачи снижается в два раза, в результате чего глубина рекурсии составляет log²n.

Оценка времени работы алгоритма умножения чисел

Рекурсивные вызовы процесса умножения приводят к образованию дерева. При каждом вызове происходит некоторое число расчетов, плюс выполняются 3 рекурсивных вызова. Общим временем работы в данном случае является сумма времени, затраченного на выполнения расчетов во всех узлах (вершинах) дерева, тогда как непосредственный процесс вызова процедур занимает гораздо меньше времени.

Главные идеи вышеописанного алгоритма неоднократно использовались при решении самых разных задач с однозначными и многозначными числами. Общая методика этого алгоритма умножения чисел получила название «разделяй и властвуй». Согласно данной технике вычисления, задачу делят на непересекающиеся подзадачи того же типа, однако меньшего размера, причем каждая подзадача вычисляется отдельно, а результаты решения в итоге объединяются в решение исходной задачи.

Можно умножать однозначные и многозначные числа ещё быстрее — за время O(n log n log log n), используя быстрое преобразование Фурье.

Источник