Современный мир беспрестанно развивается. Раньше многие понятия были сокрыты от людей, считались непонятными. Так появилось программирование с собственными алгоритмами. Специально обученные люди пользуются некими «машинными языками», чтобы создавать программы и игры, «общаться» с компьютерами и другими устройствами.
Но некоторые термины у программеров появились, благодаря точным наукам – физике, математике и так далее. Существуют так называемые рекурсивные алгоритмы, без которых продвинутому разработчику/программисту придется туго. В данной статье будет рассказано о том, что соответствующий термин значит, как используется на практике в «машинном языке».
Программирование – определение
Но перед определением упомянутого термина требуется разобраться с другими важными понятиями. Что такое программирование, о котором тоже зайдет речь, понимает далеко не каждый.
Так описывают процедуру создания компьютерных программ, игр, приложений. Основывается на применении определенного синтаксиса. А именно – языка программирования.
Сейчас есть программирование как на мобильных, так и на компьютерных платформах. Люди, занимающиеся написанием кодов программ, называются программистами.
Язык программирования
Язык программирования – некий сборник формальных правил, согласно которым пишутся всевозможные программы. Требуется для того, чтобы пользователь/программер мог «общаться» с компьютерами и другими устройствами.
Языков существует огромное множество. Каждый обладает собственным синтаксисом, функциями, операторами, посредством которых составляются выражения. Условно разделяются на:
- объектно-ориентированные;
- декларативные.
Первые просты в освоении, так как используют в процессе создания приложения независимые объекты и их группы. Декларативные языки предусматривает установление связи между информационными первоначальными структурами, а также конечным результатом.
Рекурсивные функции присутствуют в каждом языке. Если разобраться с ними, получится быстро производить различные расчеты через компьютеры, а также составлять расчетные приложения.
Рекурсия – что это такое
Рекурсией называется некое свойство объекта или вещи, позволяющее заниматься подражанием самому себе. Предмет рекурсивный, если его части обладают такой же «внешностью», как и весь он целиком. Имеет широкое распространение в математике, физике, написании машинных кодов.
В случае с компьютерами упомянутым свойством обладают преимущественно функции. Они также зовутся методами.
Рекурсией при подобных обстоятельствах называют способ определения функций, при котором результат возврата для соответствующего аргумента определится на основе результатов возврата из этой же функции для предыдущего (того, что больше или меньше) значения аргумента.
Когда метод вызывает себя самостоятельно, он носит название «рекурсивный алгоритм» или «вызов». Каждый раз будут запоминаться прошлые значения внутренних локальных переменных, а также полученных в результате расчетов параметров функций.
Для того, чтобы каждый шаг рекурсивного вызова отличался от прошлого, корректируются параметры функции. Минимум – один из них. Останавливается процесс соответствующих алгоритмов тогда, когда корректируемые значения достигают некоторого «лимита». Пример – обработка последнего массивного элемента.
Выражение в компьютерах
Программеры сталкиваются с рекурсивными алгоритмами в структурах данных:
- Графы. Эти объекты рассматривают в качестве совокупности отдельных узлов и подграфов (наименьших из имеющихся).
- Строки, состоящие из первого символа и подстроки. А именно – самой маленькой строчки.
Также рассматриваемое понятие встречается в шаблонах проектирования. Пример – декораторы. Его объекты могут включать в себя другие составляющие, которые тоже выступают в качестве декораторов. А еще в виде функций. Последний вариант является самым распространенным. Особенно при написании машинных кодов.
Основным правилом операции служит следующий принцип: до рекурсивного вызова обязательно должна стоять проверка на возврат.
Важные термины
Для лучшего понимания темы необходимо уяснить следующие понятия:
- Рекурсивный порядок действий – тот, в определении которого имеется прямой/косвенный вызов того же метода.
- Рекурсивная функция – математическое уточнения интуитивного понятия рассматриваемого выражения.
- Адаптивный рекурсивный алгоритм – порядок действий, при которых благодаря рекурсивности во внимание принимаются индивидуальные черты решаемой задачи из области своего определения.
- Базис – предположение, которое определяет начальные обстоятельства или «картину» происходящего в момент завершения. Здесь описывается элементарный случай, при котором удается сразу получить ответ.
- Шаг – принцип, тело которого содержит в качестве подцели вызов определяемого предиката.
- Подпрограммы – все то, что располагается внутри рекурсивных операций.
Теперь можно подумать, какие у рекурсии имеются разновидности. Их не так много, но каждый вариант развития событий предусматривает собственные нюансы.
Стратегия
Но для начала стоит рассмотреть так называемый рекурсивную стратегию. Это – общий случай, согласно которому происходит реализация поставленной задачи. Состоит из нескольких шагов:
- упорядочивание информации;
- решение меньшей части проблемы;
- поиск и реализация решения большей части поставленной задачи.
Для лучшего понимания стоит рассмотреть наглядный пример, но о нем позже. Ведь рекурсия и ее методы бывают разными. И каждый предусматривает какие-то свои нюансы.
Разновидности рекурсии
Рекурсивные методы классифицируются по-разному: по своей сложности или «хвостовой части». Поэтому условно разделить соответствующий элемент можно на несколько крупных категорий.
Простая
Это – функция, которая содержит вызов иных операций и методов. Способна вызывать себя самостоятельно. Никаких парадоксов. Компьютер будет последовательно выполнять команды, а если встретится вызов процедуры, займется ей.
Procedure Rec(int n);
Begin
If n>0 then;
Rec(n-1);
Writeln(n);
End;Предложенный код – пример простой рекурсии. Но есть и другие варианты развития событий. Решения задачи иногда требуют более «запутанных» алгоритмов.
Сложная
Данном случае одна функция вызывает другую. Вторая ответно занимается вызовом первой. При подобных обстоятельствах первая операция должна вызывать ту, что еще не описана. Для того, чтобы справиться с поставленной задачей, используются так называемые опережающие описания.
Procedure A(int i); //заголовок первой операции – опережающее описание
Procedure B(int i); //опережающая «характеристика» второго действия
Procedure A(int i); //полное описание основной операции A
Begin
Writeln(i);
B(i-1);
End;
Procedure B(int i); //полное описание основной операции B
Begin
Writeln(i);
If i<10 then
A(i+2);
End;Если попытаться представить наглядно предложенные рекурсивные функции, то простой вариант – это уроборос. Сложный – детский стишок, в котором «волки с перепуга, скушали друг друга». Достаточно наглядно представить этот процесс и двух волков, чтобы понять, о чем речь.
Хвостовая
Хвостовой рекурсия будет, если соответствующий вызов окажется последним действием функции перед тем, как произойдет возврат результата. То есть, окажется в «хвосте» описываемого алгоритма:
Def fact_tailrec(n, result 1);
If n=0;
Return result 1
Else
Return fact_tailtec(n-1, result*n)Этот код актуален для факториала.
Не обязательно метод хвостового типа будет также считаться рекурсивным. Он способен вызывать иные функции, осуществлять взаимную рекурсию или иные, более сложные схемы. Каноничный пример взаимной рекурсии:

Тут вызовы функций располагаются в «хвосте». Более простым примером обойтись нельзя. Связано это с тем, что представленные коды используют только один вызов в каждой операции. Кодификация усложняется, когда необходимо осуществлять множественные обращения. Пример – вычисление числа Фибоначчи.
Не хвостовая
Если же вызовы не являются последними в задействованной функции, она называется не хвостовой. Таких примеров очень много. Все, что не относится к хвостовому виду.
Классификация по записи
Рекурсивная функция может вызывать сама себя. Из-за этого приходится повторно выполнять имеющиеся в ней указания. Происходит операция, подобная работе цикла. Записываться такой элемент может разными методами:
- Префиксным способом. Сначала происходит рекурсивный вызов, только потом – необходимые действия.
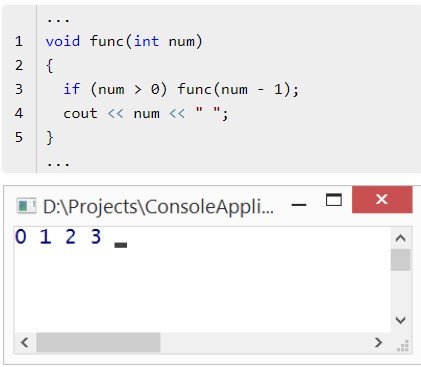
- 2. Постфиксной записью. При подобных обстоятельствах на первый план выходят те или иные алгоритмы/манипуляции. Лишь после программист должен сделать вызов рекурсивной функции.
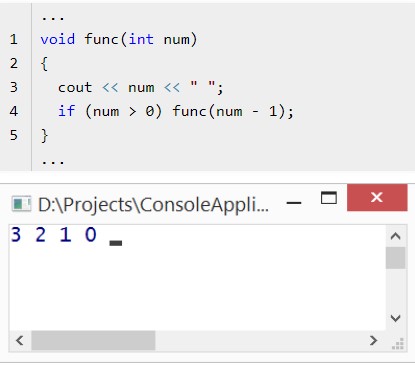
Стоит обратить внимание на некоторые «частные» случаи. Они помогают заменить рассматриваемые типы записей на более простые.
Итерирование
Отдельный вид рекурсии – когда в его основе находятся рекуррентные соотношения. Они имеют вид:
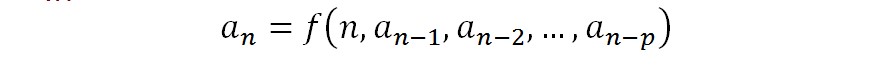
Здесь каждый элемент последовательности выражается через p предыдущих членов. Для того, чтобы получить тот или иной результат, потребуется повторение обновления значений этой самой последовательности. Соответствующее действие называют итерацией, а сам процесс «воспроизведения» — итерирование.
Итерация – осуществление обработки информации, при которой предпринимаемые манипуляции повторяются много раз. Вызов элементов массива (то есть, самих себя) в описываемом случае не осуществляется. В рекурсии – да.

При вызове функций осуществляется некоторое количество допрасходов, связанных с передачей управления и аргументов, возврата вычисленных значений. Итерационная операция в случае с факториалом (пример выше) окажется быстрее recursion. Итерация c рекурсией не всегда совместимы.
Внимание: если в основе рекурсивной операции лежит единственное условие «вызвать саму себя», ее удастся с легкостью заменить итерационным циклом.
Алгоритмы рекурсии – анализ
Когда происходит анализ циклических функций, осуществляется расчет трудоемкости итераций и их численность в самом плохом, хорошем и среднем случае. Но с рекурсией подобный расклад не работает. Связано это с тем, что в конечном итоге получится рекуррентное соотношение. По ним сложность оценить невозможно.
Поэтому на практике используются различные способы реализации поставленной задачи:
- Подстановка (метод итераций). Последовательно заменяются рекуррентные части в выражениях для того, чтобы получить новые. Операция не прекращается до тех пор, пока не будет понят общий принцип, а также пользователь не сможет переписать его нереккурентной формулой. В примере ниже выведена формула, но первый шаг – это предположение. Нет никаких доказательств соответствия операции рекуррентному выражению.
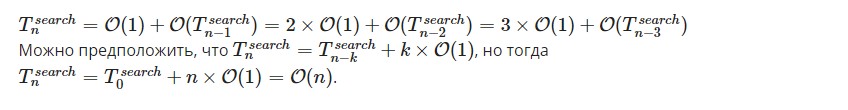
- 2. Математическая индукция. Доказывает истинность некоторого утверждения, состоящего из двух шагов. Первый – это доказательства утверждения для частных случаев (одного или нескольких). Второй – из истинности основополагающего утверждения (индуктивной гипотезы) и частных случаев выводят подтверждение последующих шагов.
- 3. Общий. В нем каждое условие для случая в формуле доказано формально. Требуется определить случай основной теоремы, согласно которому обнаружится соответствие рекуррентного соотношения.
Но приведенные примеры преимущественно встречаются в теории. В реальной жизни они не имеют места. Для лучшего понимания рекурсии стоит изучить наглядный практический пример. Он пригодится каждому пользователю.
Пример из практики
Решения рекурсивного характера – условие, которое не так трудно обнаружить на практике. Но жизненные примеры весьма проблематично представить такими, чтобы их можно было изобразить итеративным способом.
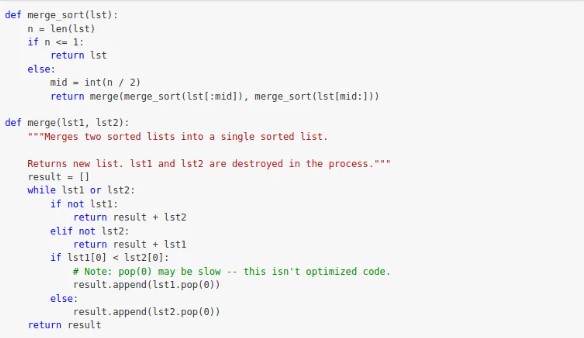
Это – наглядный образец сортировки посредством слияния. Используемый язык программирования – Python. Чем-то напоминает обратный ход дерева – сначала требуется пойти рекурсивно влево, после – вправо, далее – скомбинировать полученные результаты. Подобные вариации в «обычный» код перерабатываются с трудом. Но в практике применяются достаточно часто.
Сортировка посредством слияния – множественная рекурсия, которая была рассмотрена равным образом как с числом Фибоначчи.
Теперь основные моменты, связанные с рекурсией в программировании, понятны. Более углубленное изучение темы основывается на составлении различных примеров непосредственно на языках программирования.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!







