В математике существует немалое количество важных элементов и значений для проведения расчетов. Некоторые из них изучаются в школах, а какие-то – в ВУЗах. Немаловажной составляющей является матрица.
Далее речь зайдет об этой математической единице – что она собой представляет, для чего необходима, какие действия с ней выполняются.
Что это
Матрица представляет собой прямоугольную таблицу элементов. Это – своеобразная таблица чисел.
Некий математический объект, который записывается в виде прямоугольной таблице элементов кольца или поля. Он представлен совокупностью строк и столбцов, на пересечении которых располагаются числа. Последний – его компоненты.
Размер матрицы определяется количеством строк и столбцов. Исторически существуют разнообразные «предметы» данного типа. Пример — треугольные. Сейчас каждым математиком изучаются понятия квадратной матрицы и прямоугольной.
Возможные действия
С рассматриваемыми объектами можно выполнять различные действия:
- сложение;
- вычитание;
- умножение числа на заданную матрицу;
- нахождение определителя;
- комплексное сопряжение.
Далее поможем разобраться со всеми этими алгебраическими манипуляциями с наглядными примерами. Предложенная информация пригодится не только математикам, но и программистам.
Сложение
Складывать можно только матрицы, которые содержат в своем составе одинаковое количество чисел. Результатом будет служить объект такого же размера.
Чтобы провести операцию, требуется просто сложить их соответствующие компоненты. Пример приведен ниже.
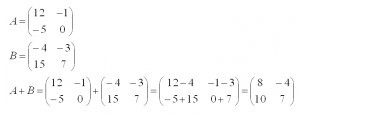
Здесь манипуляции проделывались через матрицы a и b размером два на два. Сложение происходит и относительно положительных чисел, и относительно отрицательных.
Вычитание
При решении задач по математике, связанных с рассматриваемой темой, важно помнить об элементарных действиях. Вычитание производится по тем же принципам, что и сложение. На выходе получается матрица аналогичного размера.
Умножение на число
Любую матрицу допустимо умножить на произвольное число. Для этого предстоит:
- умножить каждый элемент оной на заданное число;
- произвести запись объекта с новыми данными.
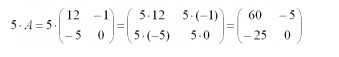
Выше представлен пример умножения числа на заданную матрицу.
Между собой
Также в математике можно перемножать между собой рассматриваемые объекты. Но умножение матриц друг с другом представляется возможным не всегда.
Такая операция допускается, если число столбцов в объекте A равно числу строк объекта B. Каждый элемент, получившийся в i-ой строке и j-м столбце – это сумма произведений соответствующих компонентов в i-й строчке первого множителя и j-м столбце второго.
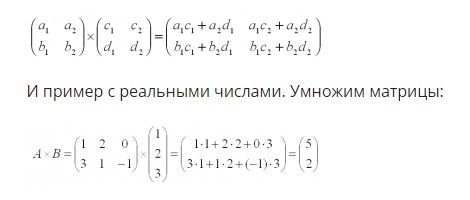
Все это – примеры того, как математик умножает рассматриваемые объекты между собой. Первый случай – теоретическая запись, второй – наглядное решение.
Транспонирование
Умножение числа на заданную матрицу – это не трудно. Но есть еще транспонирование. Так называют операцию, когда строки и столбцы меняются местами.
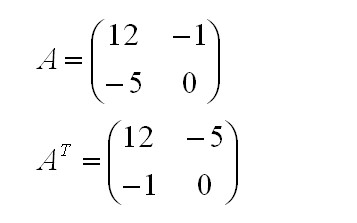
Выше – запись транспортированного объекта.
Определитель
Как осуществлять сложение двух матриц, а также их умножение, понятно. Достаточно помнить базовые алгебраические правила. Но рассматриваемый компонент может иметь определитель. Его также называют детерминантом. Встречается в линейной алгебре.
Определитель – численная характеристика квадратной матрицы. Она необходима для решения большого количества задач.
Для поиска определителя требуется вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка (состоящей из одного компонента) – это то самое число, что в ней содержится. Если объект размером 3×3, справиться будет сложнее.
Для проведения расчетов необходимо запомнить, что:
- Значение определителя будет равно сумме произведений главной диагонали и произведений элементов, лежащих на треугольниках с гранью параллельной главной диагонали.
- От последней нужно вычесть произведение элементов побочной диагонали и произведение составляющих, лежащих на треугольниках с гранью параллельной побочной диагонали.
- На практике определители крупных матриц необходимо в исключительных случаях.

Выше представлен пример нахождения детерминанта в квадратном объекте 2×2.
Обратные «модели»
Обратная матрица тоже встречается при решении задач. Вырожденная «модель» — это квадратный объект строк и столбцов n-го порядка, когда определитель равен нулю. Невырожденная – когда не равен ему соответственно.
Матрица A-1 – обратная, если для нее актуально соотношение типа: A x A-1=A-1 x A = E.
Если A-1 не вырождена, то существует всего одна обратная матрица A-1. Она будет равна значению:

А вот несколько наглядных примеров:
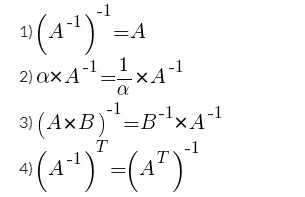
Как найти
Для того, чтобы определить A-1, необходимо:
- Найти детерминант A.
- Проверить, чтобы он не был равен нулю.
- Найти миноры матрицы – Mij.
- Определить Aij= (-1)i+jMij.
- Построить матрицу алгебраических дополнений:

- Поделить каждое из слагаемых (каждый элемент матрицы) объекта на детерминант A.
Умножение числа на матрицу, как и другие операции – это не так трудно. Зная соответствующую базу, человек сможет производить вручную или через специальные калькуляторы необходимые подсчеты. А некоторые видео уроки объяснят теорию простым языком.
Как лучше разобраться в теме
Для того, чтобы лучше понимать рассматриваемую тему, можно отправиться на специализированные IT-курсы. Там помогут:
- получить практику;
- освоить разнообразные направления математики и информационных технологий;
- обзавестись новыми полезными знакомствами;
- заниматься максимально комфортно – в удобное время, через интернет.
В конце обучения выдается сертификат, подтверждающий знания в выбранном направлении. Предложения есть как для новичков, так и для продвинутых математиков/разработчиков/системных администраторов.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:







