Бинарный поиск: описание и принцип реализации в программировании

В компьютерной деятельности поиск – одна из наиболее выполняемых операций. Позволяет обнаружить элемент, соответствующий установленным заранее параметрам. Для среднестатистического пользователя процедура выглядит простой: в поисковой строке он задает критерии искомого объекта, а затем воплощает их в жизнь.

В программировании ситуация обстоит иначе. Для поиска можно использовать разнообразные методы сортировки данных. Пример – алгоритм бинарного обнаружения. О нем и пойдет речь далее.

Определение

Поиск бинарного типа – простой вариант обнаружения искомого элемента, понятный на интуитивном уровне. Отличается высокой эффективностью. Может быть использовать только в отсортированном массиве информации. Отсюда следует, что перед тем, как активировать алгоритм, иногда требуется предварительная обработка имеющихся электронных материалов.

Двоичный поиск – классический вариант обнаружения элемента в массиве (векторе), в котором применяется принцип дробления на половинки. Может быть использован в:

• информатике;
• математическом программировании;
• математике вычислительного характера.

Такой алгоритм носит название дихотомии или «метод деления пополам».

Принцип функционирования

Рано или поздно почти каждый математик и программист задумываются над тем, как работает алгоритм бинарного поиска заданного элемента. Здесь каждый раз используется принцип «разделяй и властвуй». С его помощью массив будет разделен пополам при проверке, подходит ли элемент массива под искомый.

При помощи такого подхода желаемое значение обнаруживается достаточно быстро и легко. Сложная задача будет раздроблена на простые линейные операции, в котором мы ищем заданный заранее элемент. Упрощение производится до тех пор, пока поставленная задача не сможет быть решена напрямую.

Описание принципа работы

Работает двоичный поиск легко и просто. Дан заранее отсортированный массив информации, где элементы отсортированы по возрастанию. Чтобы обнаружить в нем конкретные данные, потребуется выполнить следующее:

1. Найти средний элемент заданного массива информации.
2. Сравнить полученный объект со значением, которое мы ищем (с так называемым ключом). Если оный меньше среднего элемента, поиск осуществляется в левой половине. В противном случае – в правой.
3. Когда ключ имеет такое же значение, что и средний элемент, происходит возврат индекса оного.
4. Продолжать выполнять 1-2 шаги до тех пор, пока не останется один объект.
5. Когда программа дойдет до последнего элемента, а ключ так и не был обнаружен, происходит возврат -1.

Для такого линейного поиска рекомендуется рассмотреть наглядный пример из обыденной жизни.

Наглядный пример

У многих программистов и математиков возникает вопрос относительно того, почему нельзя просто при работе выбранного алгоритма отбрасывать половину текущего диапазона при проверке объекта. Получается следующая картина:

1. Пусть будет дан массив: 1, 2, 5, 7, 13, 15, 16, 18, 24, 28, 29.
2. Обнаружить необходимо число 18.
3. Середина массива – это 15.
4. 18 больше 15, поэтому обнаружение требуется производить в правой части.
5. Продолжение операции будет происходить в отношении ряда: 16, 18, 24, 28, 29.

Теперь по первому разбиению можно продолжать работу с массивом до обнаружения элемента или одного кандидата на ключ:

1. Работать предстоит с числовым рядом: 16, 18, 24, 28, 29.
2. Середина – 24.
3. 18 меньше 24, поэтому работать предстоит с левой частью.
4. На выходе получается выбор между 16 и 18.
5. 18 больше 16. Нужно работать с правым «блоком» массива.
6. 18 равно 18. Искомый элемент обнаружен.

Результат – один возможный кандидат на ключ при поиске. Он соответствует искомому элементу. В приведенном примере для того, чтобы найти правильный ответ, потребовалось не очень много вычислений. Для поставленной зачади использовались 4 сравнительных шага. Они помогли обнаружить элемент в множестве 11 компонентов.

Реализация в программировании

Теперь можно изучить простой код, при помощи которого удастся осуществлять двоичный поиск в программировании. Сделаем пример на языке Java, а точнее – Javascript. Binary Search будет выглядеть так:

function binarySearch(sortedArray, key){
    let start = 0;
    let end = sortedArray.length - 1;

    while (start <= end) {
        let middle = Math.floor((start + end) / 2);

        if (sortedArray[middle] === key) {
            // found the key
            return middle;
        } else if (sortedArray[middle] < key) {
            // continue searching to the right
            start = middle + 1;
        } else {
            // search searching to the left
            end = middle - 1;
        }
    }
	// key wasn't found
    return -1;
}

Здесь происходит следующее:

1. Текущий подмассив составляющих отслеживается через две переменные – start и end.
2. В заданном количестве элементов находим средний.
3. Происходит проверка среднего «компонента» с key.
4. За счет того, что множество информации было отсортировано, допускается отбрасывание половины элементов их него. Достигается это за счет изменения переменных star или end. Все зависит от того, где будет происходить дальнейший поиск. Если у правой границы – end, в противном случае – start.
5. Когда элемент, на который смотрит функция, меньше заданного заранее ключа, нужно скорректировать key на middle +1. Это поможет эффективно отбросить текущий компонент и все объекты, которые меньше него.

Предложенный подход в Java используется в основном для работы с массивами целых чисел. Аналоги алгоритма имеются и в других языках программирования. В C++:

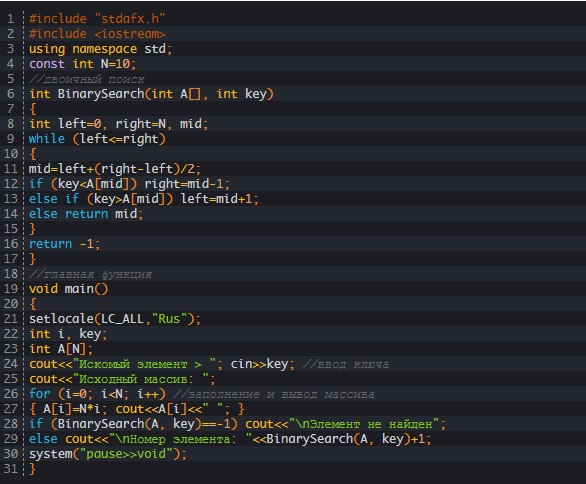
В Pascal:

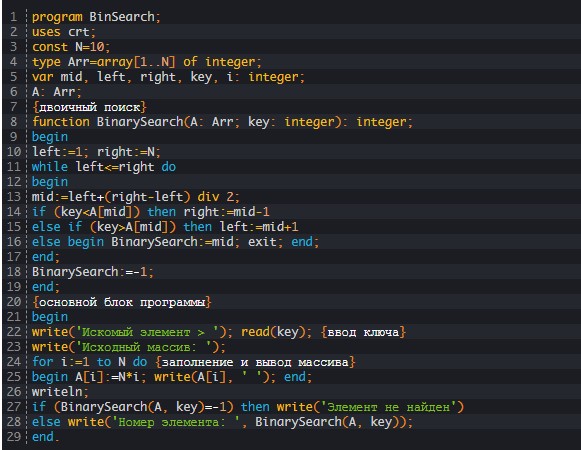
Несколько слов об эффективности

Бинарный поиск не всегда эффективен. В процессе его работы возникают некоторые сложности. Временная «трудность» составляет O (log2 n), где n выступает количеством компонентов в заданном множестве. Это не такое большое значение. Во время классического линейного поиска имеет место временная сложность O (n).

Стоит запомнить следующие данные о рассматриваемом методе:

1. Бинарный подход относится к алгоритмам на месте. Работает с исходным множеством значений, не создавая никаких копий в процессе функционирования.
2. Действует исключительно с заранее отсортированными данными.
3. Сложность сортировки высокой эффективности составляет O (nlogn).
4. Из вышесказанного следует, что, если процедуру обнаружения выполняют только один раз, рекомендуется применять алгоритмизацию грубой силы (пример – линейный поиск).

Рассмотренный прием обладает высокой эффективностью, если требуется производить повторное обнаружение в крупных множествах информации. В случае с 11 компонентами потребовалось всего 4 шага. Но для того, чтобы искомый объект был найден в множестве из 10 000 000, для проверки использовались бы всего 24 составляющие. Это – 0, 0002% от всего массива информации.

Вместо заключения

Теперь понятно, как работает рассмотренный бинарный поиск на примере с Java. Аналогичный алгоритм встречается во всех языках программирования. Он отличается особой эффективностью в большинстве случаев. Но для того, чтобы он мог нормально функционировать, предстоит перед началом работы с массивом провести его сортировку тем или иным способом.

А для того, чтобы научиться лучше программировать и понимать сложные кодификации, можно посетить специализированные компьютерные курсы. Они:

1. Организовываются дистанционно. Можно пользоваться оными в любое удобное пользователю время.
2. Имеют множество направлений. Осваивать допускается как одно из них, так и сразу несколько.
3. Обладают разным уровнем сложности. Есть предложения для новичков и продвинутых программистов.
4. Предлагают бесценную практику и поддержку хорошими кураторами.

Программы рассчитаны на срок от нескольких месяцев до года. По окончании выдается сертификат установленного образца, подтверждающий знания в выбранном направлении.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Также, возможно, вам будет интересен следующий курс: