Случайные величины и средства абстракции

Случайная величина представляет собой функцию, переводящую элементарные исходы в вещественные числа. Например, в уже рассмотренной ранее задаче можно ввести случайную величину ρ(ω), то есть расстояние от центра мишени до точки попадания. Простота такой модели позволит явно задавать пространство элементарных исходов: 

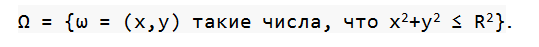
В таком случае случайная величина будет равна:

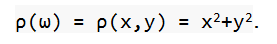
Средства абстракции и функция распределения

Хорошо, если структура пространства хорошо известна, однако на практике так бывает, увы, не всегда. Но даже если структура пространства будет вам известна, она может быть чрезвычайно сложна. Чтобы описать случайные величины, когда их выражение неизвестно, есть понятие функции распределения.

Функцию распределения обозначают F_ξ(x) = P(ξ < x) (здесь нижний индекс ξ означает случайную величину). Таким образом, речь идет о вероятности множества всех таких элементарных исходов, причем таких исходов, для которых значение случайной величины ξ на данном событии меньше, чем заданное значение x.

Какие свойства характеризуют функцию распределения:

1. Она находится между нулем и единицей.
2. Когда ее аргумент х растет, она не убывает.
3. Если число -x очень велико, функция распределения будет близка к нулю, а если само х большое, то функция распределения будет близка к единице.

По всей вероятности, смысл данной конструкции при первом чтении будет не очень понятен. Однако стоит вспомнить одно из полезных свойств функции распределения — она дает возможность искать вероятность, что величина принимает значение из интервала. Представим, что P (случайная величина ξ, принимающая значения из интервала [a;b]) равняется F_ξ(b)-F_ξ(a). На основании этого равенства мы можем выполнить исследование и узнать, каким образом изменится данная величина, если границы интервала a и b будут близки.

Итак, пусть d = b-a, в таком случае b = a+d. Следовательно, F_ξ(b)-F_ξ(a) = F_ξ(a+d) — F_ξ(a). Если значения d будут малы, то указанная выше разность будет так же мала (в случае, когда распределение непрерывное). Тут есть смысл рассмотреть следующее отношение:

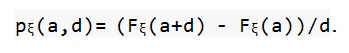
И если при относительно небольших значениях d это отношение будет совсем незначительно отличаться от константы p_ξ(a), не зависящей от d, то в данной точке случайная величина будет иметь плотность, равную p_ξ(a).

Итак, сейчас смысл функции распределения мы можем определить следующим образом: ее производная (то есть плотность p_ξ, которая была определена выше) в точке а описывает, как часто случайная величина станет попадать в небольшой интервал с центром в точке а (речь идет об окрестности точки а), если сравнивать с окрестностями иных точек. То есть чем быстрее возрастает функция распределения, тем выше вероятность появления такого значения во время случайного эксперимента.

Идем дальше. У нас есть возможность произвести вычисления функции распределения для случайной величины ρ(ω) = ρ(x,y) = x²+y², обозначающей расстояние от точки случайного попадания в мишень до центра.

Давайте вспомним определение:

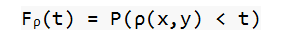
То есть наше множество {ρ(x,y) < t)} включает в себя такие точки (x,y), расстояние от которых до 0 меньше, чем t. Мы уже рассчитывали вероятность данного события, когда оценивали вероятность попадания в «десятку» — эта вероятность равняется t²/R². Следовательно, для 0<t справедливо следующее:

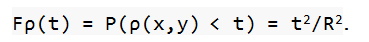
У нас есть возможность рассчитать плотность p_ρ данной случайной величины. Важно сказать, что вне интервала [0,R] плотность будет нулевой, т. к. функция распределения на данном промежутке будет неизменна. А вот на концах интервала плотность не определена. Зато внутри интервала плотность можно найти с помощью таблицы производных и простейших правил дифференцирования. Таким образом, производная от t²/R² будет равна 2t/R². Это значит, что плотность найдена на всей оси вещественных чисел.

Очередное полезное свойство плотности — это вероятность, что функция принимает значение из промежутка и вычисляется посредством интеграла от плотности по данному промежутку.

В первом чтении интеграл по промежутку [a; b] от нашей функции f(x) мы можем представить в качестве площади криволинейной трапеции. Стороны — фрагмент оси Ох, промежуток [a,b] (горизонтальная ось координат), вертикальные отрезки, которые соединяют точки (a,f(a)), (b,f(b)) на кривой с точками (a,0), (b,0) на оси Ох. Последняя сторона — это фрагмент графика функции f от (a,f(a)) до (b,f(b)).

Мы можем говорить об интеграле по следующему промежутку: (-∞; b], но только тогда, когда для довольно больших отрицательных значений a значение интеграла по [a;b] будет меняться пренебрежимо мало, если сравнивать с изменением числа a. Аналогично определяют и интеграл по таким промежуткам, как [a;+∞), (-∞,∞).

Последнее немаловажное свойство плотности заключается в том, что интеграл от плотности любой случайной величины будет равняться 1. Трактовка проста: вероятность, что функция примет любое значение, равняется 1. Вдобавок к этому, в случае вычисления интегралов от плотностей случайных величин, значения которых будут лежать в ограниченном промежутке, следует брать интеграл лишь по этому промежутку.

По материалам статьи «Математика для программистов: теория вероятностей».