В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.
Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.
Обозначение квадрата осуществляется с помощью степени, то есть Х² читается «Х в квадрате».
Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х2:
Х2 = Х ⋅ Х
Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.
Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:
32 = 3 ⋅ 3 = 9
52 = 5 ⋅ 5 = 25
102 = 10 ⋅ 10 = 100
Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.
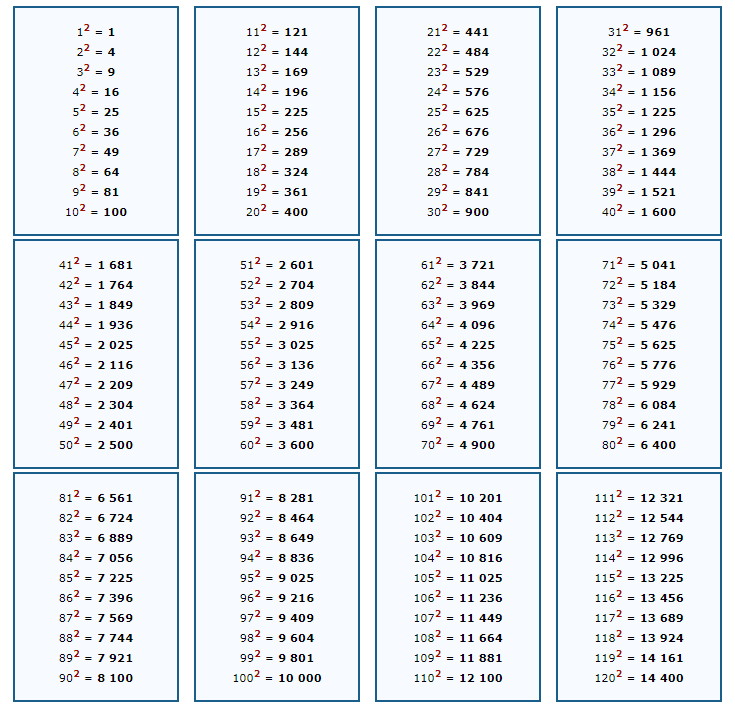
Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.
Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):
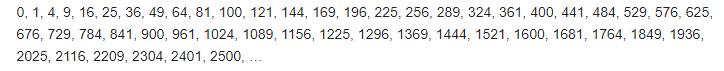
Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.
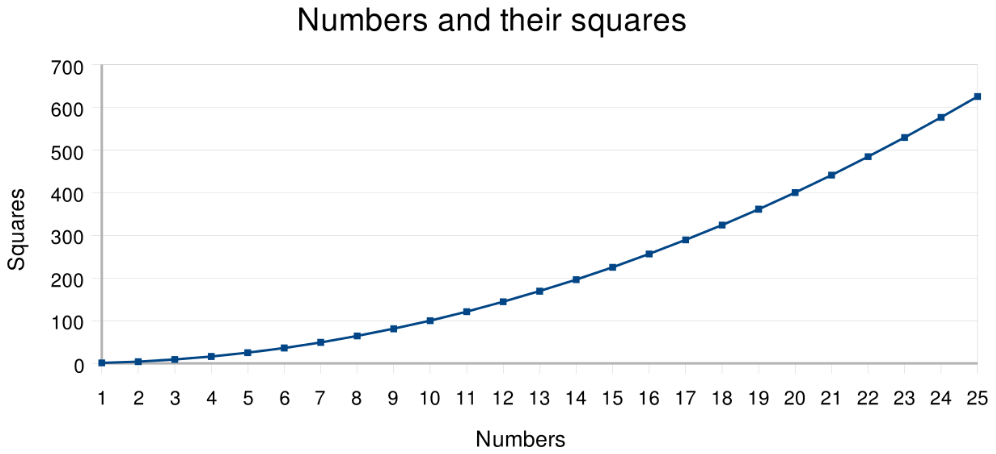
Квадратные числа
Если же говорить о натуральных числах из последовательности, упомянутой выше, в историческом контексте, то их всегда называли «квадратными». Квадратное числовое значение также называют полным либо точным квадратом, то есть целым значением, квадратный корень из которого можно извлечь нацело. К примеру, найти корень из 9 несложно (√9 = 3, т. к. 3 ⋅ 3 = 9). Не составляет проблем и вычислить корень из ста: (√100 = 10, ведь десять на десять равно сто).
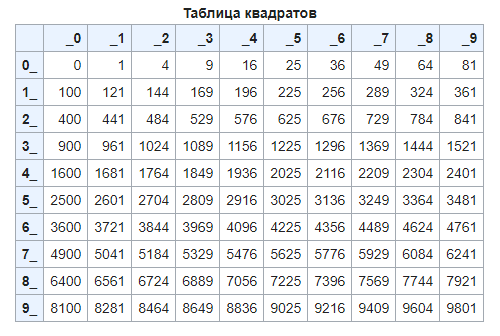
Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10, плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.
А что в программировании?
Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).
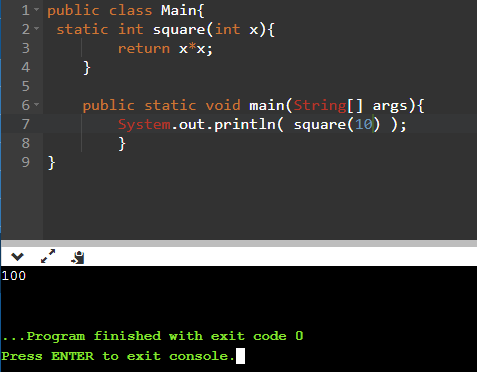
Напишем простой метод по возведению любых числовых значений в квадрат:
public class Main{
static int square(int x){
return x*x;
}
public static void main(String[] args){
System.out.println( square(10) );
}
}
Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.
Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:
public class Main{
public static void main(String args[]){
double x = 100;
System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));
}
}
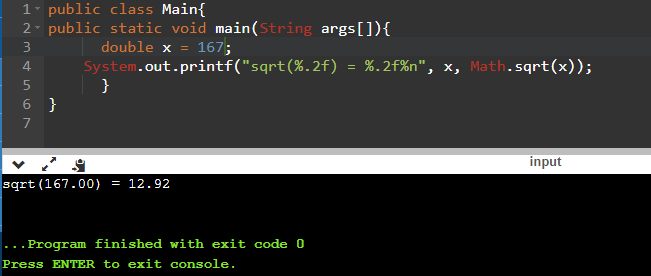
Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:
Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

По материалам:
- https://calculator888.ru/tablitsa-kvadratov;
- http://www.for6cl.uznateshe.ru/kvadrat-chisla/;
- https:/ru.wikipedia.org/.



