Бинарное дерево — что это? B-деревья
Статья расскажет о том, что такое бинарные деревья. Будут представлены способы их представления и основные термины. Отдельное внимание будет уделено B-дереву и его отличию от двоичных структур.
Деревом называют структуру данных, которая имеет древовидный вид, то есть характеризуется наличием набора связанных узлов. Бинарное дерево — это конечное множество элементов, связанных с двумя разными бинарными деревьями — правым и левым поддеревьями.
Способ представления:
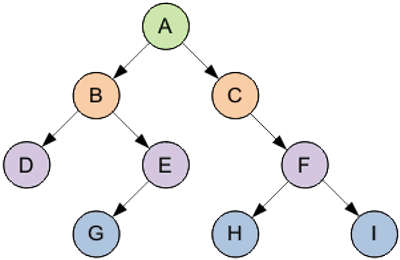
На что следует обратить внимание: — А — корень дерева; — B — корень левого поддерева и предок D; — С — корень правого поддерева; — D — потомок родительского узла B; если D располагается на уровне i, то B – на уровне i-1.
Необходимо выделить следующие термины: — узел (вершина) — это каждый элемент бинарного дерева; — ветви — связи между узлами; — глубина (высота) — наибольший уровень какого-нибудь элемента; — лист (терминальный узел) — термин применяется, если элемент не имеет потомков; — внутренние узлы — узлы ветвления; — степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева); — длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.
Использование
На практике бинарные деревья применяются, когда в каждой точке какого-нибудь вычислительного процесса нужно принимать одно из 2-х возможных решений. Существует множество задач, решаемых таким способом. Одна из них — выполнение операции, условно говоря, X с каждым элементом дерева. X рассматривается в качестве параметра обобщенной задачи посещения всех вершин либо задачи обхода дерева. Если рассмотреть такую задачу в качестве единого последовательного процесса, то можно сказать, что отдельные вершины посещаются в определенном порядке, то есть могут считаться линейно расположенными.
Способы обхода
Предположим, что имеется дерево (не пустое), в котором A является корнем, а B и C — левым и правым поддеревьями.
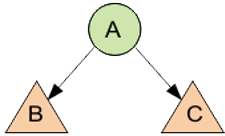
Есть 3 способа обхода: 1. Обход в прямом порядке — сверху вниз: A, B, C — префиксная форма. 2. Обход слева направо (симметричный порядок): B, A, C — инфиксная форма. 3. Обход снизу вверх (обратный порядок): B, C, A — постфиксная форма.
Реализация
На практике вершину древа можно описать в качестве структуры:
 Тогда обход в префиксной форме будет выглядеть следующим образом:
Тогда обход в префиксной форме будет выглядеть следующим образом:

Теперь инфиксная форма:

И постфиксная:

Бинарное дерево поиска
Оно представляет собой двоичное (бинарное) дерево, для которого справедлив ряд дополнительных условий. Эти условия называют свойствами:

Данные в каждой вершине должны обладать ключами, где определена операция сравнения “<”.
Обычно информация, которая представляет каждую вершину, — это запись, а не единственное поле данных.
Чтобы составить бинарное дерево поиска, пригодится функция добавления узла:

Удаляем поддерево

B-дерево. Поиск по B-дереву
В бинарном дереве поиска каждый узел содержит лишь одно значение (ключ) и не более 2-х потомков. Но существует особый вид древа поиска, называемый B-дерево (Би-дерево). Здесь узел содержит больше одного значения и больше 2-х потомков. Также его называют сбалансированным по высоте деревом поиска порядка m (Height Balanced m-way Search Tree).
B-дерево представляет собой сбалансированное дерево поиска, где каждый узел содержит много ключей и имеет больше 2-х потомков.
Возможные операции: 1. Поиск. 2. Вставка (вставляем новый элемент). 3. Удаление.
Каждое B-дерево имеет порядок. Для примера рассмотрим B-дерево порядка m. Оно будет обладать рядом следующих характеристик:

Ниже можно посмотреть на B-дерево четвертого порядка, содержащее максимум три значения ключа и максимум четыре потомка для каждой вершины.
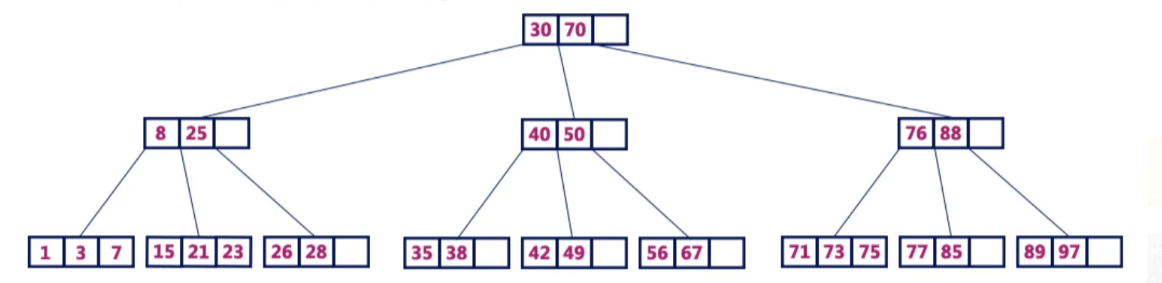
Поиск аналогичен поиску по двоичному дереву. Следует вспомнить, что в двоичном древе поиск начинается с корня, причем каждый раз принимается 2-стороннее решение (пойти по правому поддереву либо по левому). В В-дереве поиск тоже начинается с корневого узла, но с той лишь разницей, что на каждом шаге принимается не 2-стороннее, а n-стороннее решение, причем n для дерева в данном случае представляет общее число потомков рассматриваемого узла. Сложность поиска такого дерева — O(log n).
Алгоритм следующий:

Также существует такое понятие, как вставка в B-дерево.
В В-дереве вставка нового элемента возможна лишь в узел-лист. То есть вставленная новая пара ключ-значение добавляется лишь к узлу-листу. Вот, как осуществляется вставка в B-дерево:

Более подробную информацию всегда можно получить на наших курсах по алгоритмам в Москве.
Источники: — https://zen.yandex.ru/media/id/5bbcbc1ba5bd5400a990e7d9/struktura-dannyh-bderevo-5d273e1dcfcc8600ac055454; — https://prog-cpp.ru/data-tree/.